Conexiones de cuatro bombillas
De Laplace
Contenido |
1 Enunciado
Se dispone de cuatro bombillas, A, B, C, D. El etiquetado de estas bombillas indica que, para un voltaje de 120V, sus potencias nominales son respectivamente 30W, 60W, 120W y 40W. Se montas la cuatro bombillas en el siguiente esquema y se aplica entre los extremos una diferencia de potencial de 120V.
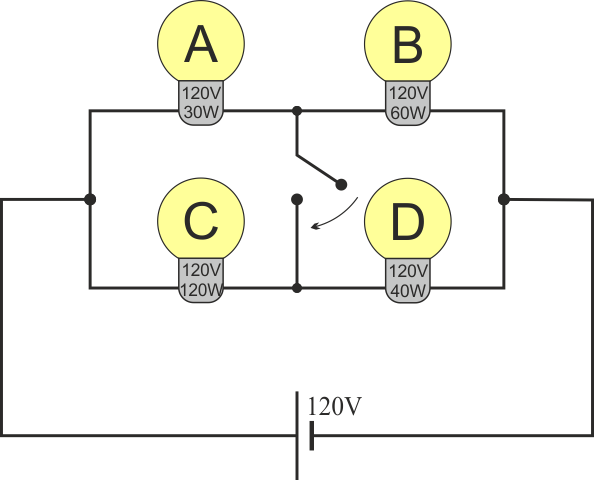
- Calcule el consumo de cada bombilla (en vatios) para este montaje, así como el consumo total del montaje. ¿Cuál es la que da más luz? ¿Y la que menos?
- Suponga que se cierra el interruptor central. Una vez cerrado, ¿cuál es el nuevo consumo total y el individual? ¿Cuál es ahora la bombilla más brillante y la menos brillante?
2 Resistencia de cada bombilla
Este problema se reduce a calcular las potencias disipadas en una serie de resistencias. Para resolverlo, primero debemos calcular los valores de éstas, empleando las potencias nominales.
Cuando en un aparato eléctrico (una bombilla, una plancha, una estufa) sus especificaciones indican valores como 120V 40W, queiere decir que si aplica una diferencia de potencial de 120V entre sus terminales, la potencia que consume es de 40W. Puesto que la potencia consumida en una resistencia por efecto Joule verifica
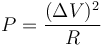
obtenemos la resistencia de cada bombilla como
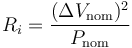
esto nos da, para las cuatro0 bombillas






