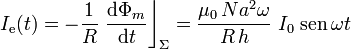Espira en el interior de un solenoide (F2GIA)
De Laplace
Contenido |
1 Enunciado
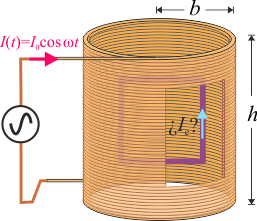
Un solenoide constituido por N espiras compactas paralelas, con forma de cilindro recto de longitud h mucho mayor que su radio b, es recorrido por una corriente eléctrica de intensidad variable en el tiempo según la ley I(t) = I0cos(ωt), siendo I0 y ω constantes conocidas. En el interior del solenoide hay una pequeña espira cuadrada de resistencia eléctrica R, autoinducción despreciable y lado a, menor que el radio b. Esta espira está contenida en un plano perpendicular a las espiras del solenoide. ¿Cuál es el valor de la intensidad de corriente Ie que recorre la espira cuadrada?2 Solución
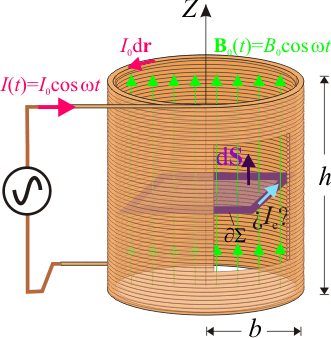
Comenzamos adoptando un sistema de referencia adecuado para proceder a la descripción analítica de las magnitudes vectoriales. Tomando el eje de la bobina cilíndrica como eje OZ de dicho sistema, se tendrá que el campo magnético producido por la intensidad I(t) que recorre el solenoide en sentido antihorario, es:

donde se ha aplicando la aproximación de bobina larga. Realmente, esta aproximación no va a suponer una pérdida de generalidad en los resultados que se obtengan para la fuerza electromotriz inducida en la espira, pues asumiremos que ésta se encuentra en el interior de la bobina, lejos de sus extremos.
En la espira cuadrada no hay conectado ningún generador, por tanto, la fuerza electromotriz responsable de que exista una corriente eléctrica en la espira  es la inducida por la variación del flujo magnético a través de ella. Si la espira tiene una resistencia eléctrica R y autoinducción despreciable, la intensidad de la corriente inducida es:
es la inducida por la variación del flujo magnético a través de ella. Si la espira tiene una resistencia eléctrica R y autoinducción despreciable, la intensidad de la corriente inducida es:

La superficie de integración Σ es cualquiera delimitada por la espira cuadrada  ; por ejemplo, el cuadrado de lado a contenido en el plano de la espira. Según se indica en el enunciado, dicho plano es perpendicular a los de las N espiras que constituyen la bobina o solenoide. En consecuencia, se tendrá que,
; por ejemplo, el cuadrado de lado a contenido en el plano de la espira. Según se indica en el enunciado, dicho plano es perpendicular a los de las N espiras que constituyen la bobina o solenoide. En consecuencia, se tendrá que,
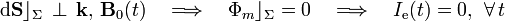
3 Anexo
Aunque no es lo que se pide en el enunciado, calculemos el valor de la intensidad de la corriente inducida en la espira si se coloca contenida en un plano paralelo a los de sus espiras. En esta situación, se tendría que
si se coloca contenida en un plano paralelo a los de sus espiras. En esta situación, se tendría que 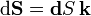 ; además, si la espira está en el interior de la bobina, lejos de los extremos, en todos los puntos de la superficie Σ habría el mismo campo magnético
; además, si la espira está en el interior de la bobina, lejos de los extremos, en todos los puntos de la superficie Σ habría el mismo campo magnético  ; entonces...
; entonces...
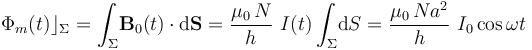
Aplicando la ley de inducción electromagnética, se obtiene que la intensidad de la corriente inducida en la espira sería: