Campo magnético en eje de espira circular (F2GIA)
De Laplace
1 Enunciado
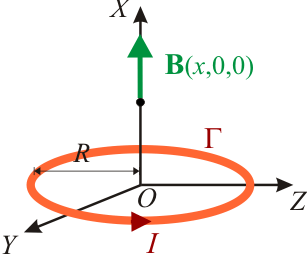
Una espira de corriente circular de radio R se encuentra contenida en al plano OYZ siendo su eje de simetría el eje OX. Suponiendo que el sentido de la corriente es antihorario visto desde un punto de la región del espacio x > 0, calcular el campo magnético creado por la espira en los puntos del eje OX.2 Solución
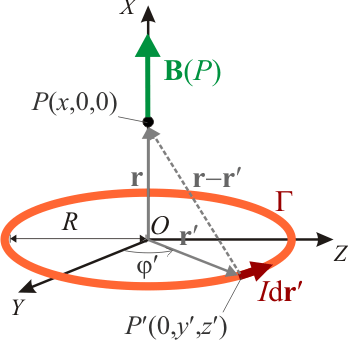
La ley de Biot y Savart establece que una corriente electrica de intesidad I que recorre una espira filiforme Γ, crea un campo magnético  , que viene dado por la expresión:
, que viene dado por la expresión:
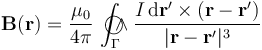
donde  es el radio-vector que determina la posición del punto P donde se evalúa el valor del campo magnético, y
es el radio-vector que determina la posición del punto P donde se evalúa el valor del campo magnético, y 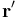 , el que indica la posición de un punto
, el que indica la posición de un punto 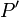 de la espira Γ donde se localiza el elemento de corriente
de la espira Γ donde se localiza el elemento de corriente 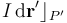 de módulo infinitesimal, dirección tangente a la espira y sentido que coincide con el de la corriente.
de módulo infinitesimal, dirección tangente a la espira y sentido que coincide con el de la corriente.
En el sistema descrito en el enunciado, donde el origen del sistema de referencia se toma en el centro de la espira circular Γ, se tendrá:
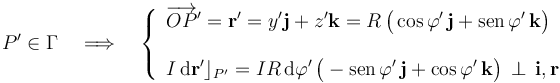
Si se quiere evaluar el campo magnético producido por la corriente de la espira en los puntos del eje OX, se tendrá...

La contribución infinitesimal al campo magnético en P(x,0,0) de cada elemento de corriente es:
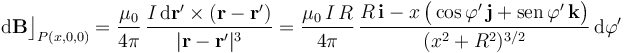
El campo magnético total en el punto P del eje OX, es igual a la superposición de todas las contribuciones de los elementos de corriente definidos a lo largo de la espira Γ:
![\mathbf{B}(x,0,0)=\int_{\Gamma}\!\!\!\!\!\!\bigcirc\!\!\!\!\wedge \mathrm{d}\mathbf{B}=\frac{\mu_0\!\ I\!\ R}{4\pi\!\ (x^2+R^2)^{3/2}}\!\ \int_0^{2\pi}\! \big[R\!\ \mathbf{i}-x\!\ \big(\cos\varphi^\prime\!\ \mathbf{j}+ \mathrm{sen}\!\ \varphi^\prime\!\ \mathbf{k}\big)\big] \!\ \mathrm{d}\varphi^\prime](/wiki/images/math/2/c/0/2c05d58a9e6fe83bfb7d8e13557d7bce.png)