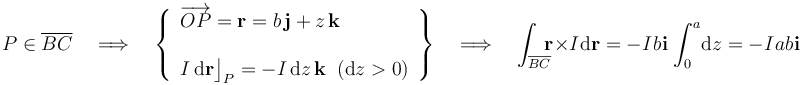Espira triangular sometida a campo uniforme (F2GIA)

De Laplace

Revisión a fecha de 22:31 29 abr 2013; Gabriel (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución
- 2.1 Fuerzas sobre cada lado de la espira
- 2.2 Momento dipolar magnético de la espira

1 Enunciado

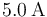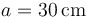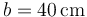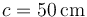Una espira de corriente que transporta una corriente de $5.0\,\mathrm{A}$ tiene forma de triángulo rectángulo con lados $a=30\,\mathrm{cm}$ , $b=40\,\mathrm{cm}\,$ y $c=50 \,\mathrm{cm}$ . Se sitúa la espira en una región donde existe un campo magnético uniforme de magnitud 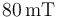$80\,\mathrm{mT}$ y cuya dirección es paralela al lado

c

. Calcular:

Fuerza ejercida por el campo magnético sobre cada lado de la espira.
Momento dipolar magnético de la espira.
Módulo del par ejercido por el campo magnético sobre la espira de corriente.

2 Solución

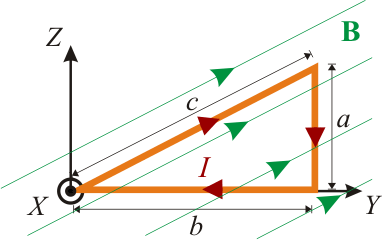
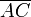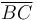Tomamos un sistema de referencia cartesiano tal que la espira $Γ$ de vértices $A$ , $B$ y $C$ , están contenida en un plano paralelo al $O Y Z$ , con los catetos $\overline{AC}$ y $\overline{BC}$ dispuestos paralelamente a los ejes $O Y$ y $O Z$ , respectivamente. La espira está sometida a un campo magnético uniforme (constante en todos los puntos del espacio), paralelo a la hipotenusa $\overline{AB}$ , y de módulo conocido:

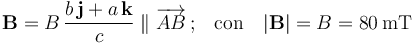
$\mathbf{B}=B\!\ \frac{b\!\ \mathbf{j}+a\!\ \mathbf{k}}{c}\; \|\; \overrightarrow{AB}\!\ \mathrm{;}\quad \mbox{con}\quad|\mathbf{B}|=B=80\,\mathrm{mT}\,$

Cuando la espira es recorrida por una intensidad de corriente 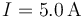$I=5.0\,\mathrm{A}\,$ , sobre los elementos de corriente 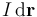$I\,\mathrm{d}\mathbf{r}$ definidos en cada uno de sus puntos, se ejercen fuerzas infinitesimales que, al sumarlas todas, producen una resultante nula:

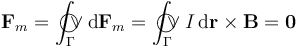
$\mathbf{F}_m=\int_{\Gamma}\!\!\!\!\!\!\bigcirc\!\!\!\!\vee \mathrm{d}\mathbf{F}_m=\int_{\Gamma}\!\!\!\!\!\!\bigcirc\!\!\!\!\vee I\,\mathrm{d}\mathbf{r}\times\mathbf{B}=\mathbf{0}$

Podemos comprobar que se cumple este resultado si calculamos las fuerzas sobre cada uno de los dados de la espira y luego los sumamos:

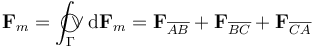
$\mathbf{F}_m=\int_{\Gamma}\!\!\!\!\!\!\bigcirc\!\!\!\!\vee \mathrm{d}\mathbf{F}_m=\mathbf{F}_{\overline{AB}}+\mathbf{F}_{\overline{BC}}+\mathbf{F}_{\overline{CA}}$

2.1 Fuerzas sobre cada lado de la espira

Obsérvese que, al estar formada por segmentos rectilíneos, el elemento de corriente en cada lado de la espira es colineal con el lado correspondiente; el sentido estará determinado por el sentido de la corriente. De esta forma, en el lado $\overline{AB}$ , se tendrá:

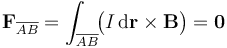
$\forall\,P\in\overline{AB}\,\mathrm{,}\,\;\;I\,\mathrm{d}\mathbf{r}\;\|\;\overrightarrow{AB}\;\|\;\mathbf{B}$ $\Rightarrow$ $\mathbf{F}_{\overline{AB}}=\int_{\overline{AB}}\!\!\big(I\,\mathrm{d}\mathbf{r}\times\mathbf{B}\big)=\mathbf{0}$

Los elementos de corriente en los catetos $B C$ y $C A$ no son colineales con el campo magnético, por lo que sobre cada uno de ellos se estará ejercienco una fuerza total no nula. Podemos aprovechar que el campo $\mathbf{B}$ es uniforme; es decir, tiene el mismo valor vectorial en todos los puntos de cada segmento, por lo que puede extraerse de las correspondientes integrales que permiten calcular las fuerzas sobre aquéllos:

$\mathbf{F}_{\overline{BC}}=\int_{\overline{BC}}\!\!\big(I\,\mathrm{d}\mathbf{r}\times\mathbf{B}\big)=I\!\ \left[\int_B^C\!\!\mathrm{d}\mathbf{r}\right] \times \mathbf{B}\,\mathrm{;}\,\qquad \mathbf{F}_{\overline{CA}}=\int_{\overline{CA}}\!\!\big(I\,\mathrm{d}\mathbf{r}\times\mathbf{B}\big)=I\!\ \left[\int_C^A\!\!\mathrm{d}\mathbf{r}\right] \times \mathbf{B}$

Y teniendo en cuenta que la suma de elementos 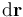$\,\mathrm{d}\mathbf{r}$ entre dos puntos es el segmento orientado definido entre dichos puntos, se obtiene:

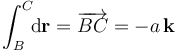
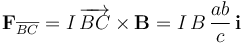
$\int_B^C\!\!\mathrm{d}\mathbf{r}=\overrightarrow{BC}=-a\!\ \mathbf{k}$ $\Rightarrow$ $\mathbf{F}_{\overline{BC}}=I\!\ \overrightarrow{BC}\times\mathbf{B}=I\!\ B\!\ \frac{ab}{c}\!\ \mathbf{i}$

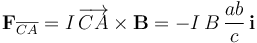
$\int_C^A\!\!\mathrm{d}\mathbf{r}=\overrightarrow{CA}=-b\!\ \mathbf{j}$ $\Rightarrow$ $\mathbf{F}_{\overline{CA}}=I\!\ \overrightarrow{CA}\times\mathbf{B}=-I\!\ B\!\ \frac{ab}{c}\!\ \mathbf{i}$

Efectivamente, se obtiene que la fuerza resultante que actúa sobre toda la espira triangular es nula:

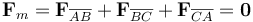
$\mathbf{F}_m=\mathbf{F}_{\overline{AB}}+\mathbf{F}_{\overline{BC}}+\mathbf{F}_{\overline{CA}}=\mathbf{0}$

2.2 Momento dipolar magnético de la espira

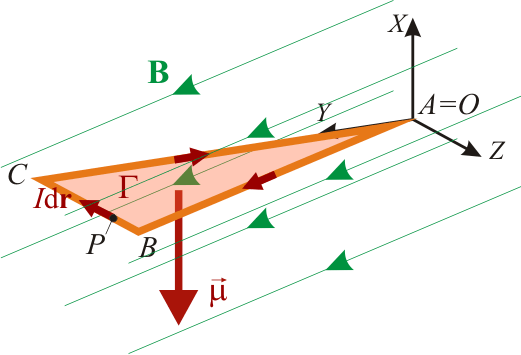
Dada la espira $Γ$ , recorrida por una corriente eléctrica de intensidad $I$ , en el sentido “horario”, se define su momento dipolar magnético como:

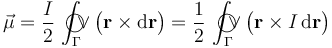
$\vec{\mu}=\frac{I}{2}\!\ \int_{\Gamma}\!\!\!\!\!\!\bigcirc\!\!\!\!\vee\big(\mathbf{r}\times\mathrm{d}\mathbf{r}\big)=\frac{1}{2}\!\ \int_{\Gamma}\!\!\!\!\!\!\bigcirc\!\!\!\!\vee\big(\mathbf{r}\times I\!\ \mathrm{d}\mathbf{r}\big)$

Tomando como centro de reducción el vértice $A = O$ de la espira triangular, 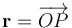$\mathbf{r}=\overrightarrow{OP}$ es el radio-vector que determina la posición, respecto de dicho centro, de un punto arbitrario $P$ de la espira $Γ$ , donde se localiza un elemento de corriente 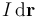$I\!\ \mathrm{d}\mathbf{r}$ . La anterior integral podemos descomponerla como la suma de las contribuciones de los lados $A B$ , $B C$ y $C A$ :

$\vec{\mu}=\frac{1}{2}\!\ \left[ \int_{\overline{AB}}\!\!\! \big(\mathbf{r}\times I\!\ \mathrm{d}\mathbf{r}\big)\!\ +\!\ \int_{\overline{BC}}\!\!\! \big(\mathbf{r}\times I\!\ \mathrm{d}\mathbf{r}\big)\!\ + \int_{\overline{CA}}\!\!\! \big(\mathbf{r}\times I\!\ \mathrm{d}\mathbf{r}\big)\right]$

Para un elemento de corriente en la hipotenusa $\overline{AB}$ , se tendrá:

$P\in\overline{AB}\quad\Longrightarrow\quad\left\{\begin{array}{l}\displaystyle \overrightarrow{OP}=\mathbf{r}\!\ \|\!\ \overrightarrow{AB}\\ \\ \displaystyle I\!\ \mathrm{d}\mathbf{r}\big\rfloor_P\!\ \|\!\ \overrightarrow{AB}\end{array}\right\}\quad\Longrightarrow\quad\int_{\overline{AB}}\!\!\! \mathbf{r}\times I\!\ \mathrm{d}\mathbf{r}=\mathbf{0}$

En el lado 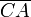$\overline{CA}$ ocurre algo análogo:

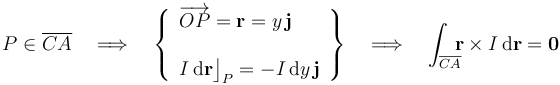
$P\in\overline{CA}\quad\Longrightarrow\quad\left\{\begin{array}{l}\displaystyle \overrightarrow{OP}=\mathbf{r}=y\!\ \mathbf{j}\\ \\ \displaystyle I\!\ \mathrm{d}\mathbf{r}\big\rfloor_P=-I\!\ \mathrm{d}y\!\ \mathbf{j}\end{array}\right\}\quad\Longrightarrow\quad\int_{\overline{CA}}\!\!\! \mathbf{r}\times I\!\ \mathrm{d}\mathbf{r}=\mathbf{0}$

La contribución del lado $B C$ si es no nula:

$P\in\overline{BC}\quad\Longrightarrow\quad\left\{\begin{array}{l}\displaystyle \overrightarrow{OP}=\mathbf{r}=b\!\ \mathbf{j}+z\!\ \mathbf{k}\\ \\ \displaystyle I\!\ \mathrm{d}\mathbf{r}\big\rfloor_P=-I\!\ \mathrm{d}z\!\ \mathbf{k}\;\;(\mathrm{d}z>0) \end{array}\right\}\quad\Longrightarrow\quad\int_{\overline{BC}}\!\!\! \mathbf{r}\times I\!\ \mathrm{d}\mathbf{r}=-I\!\ b\!\ \mathbf{i}\!\ \int_0^a\! \mathrm{d}z=-I\!\ a b\!\ \mathbf{i}$

Espira triangular sometida a campo uniforme (F2GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Fuerzas sobre cada lado de la espira

2.2 Momento dipolar magnético de la espira

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES