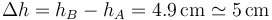Entrar Página Discusión Historial Go to the site toolbox

Calor en una expansión isoterma por un peso

De Laplace

Contenido

[ocultar]

1 Enunciado

Se tiene una balanza formada por un recipiente cilíndrico de 16 cm² de sección lleno de aire (considerado como un gas ideal). El tubo está cerrado herméticamente en su parte inferior por un émbolo que puede deslizarse sin rozamiento y que tiene un gancho en su cara inferior. Las paredes y el émbolo no están aislados térmicamente. Inicialmente el émbolo se encuentra a 15 cm de la pared superior, y el gas en equilibrio mecánico y térmico con el exterior, que se halla a 1 bar y 300 K. Se cuelga bruscamente del pistón un saco de harina de 4 kg.

  1. ¿Cuánto desciende aproximadamente el pistón hasta que se alcanza de nuevo el equilibrio?
  2. ¿Cuánto vale aproximadamente el calor que entra en el sistema en este proceso?
  3. Suponga que el saco tiene un agujero, de forma que la harina se escapa lentamente hasta vaciarse por completo (despreciamos el peso del propio saco). ¿Cuánto vale el calor que entra en el sistema en este segundo proceso?

Datos: Constante de los gases ideales: 8.314 J/K·mol; Razón de capacidades caloríficas del aire: 1.4.

2 Descenso del pistón

Este problema es muy similar al la compresión por un peso, con la diferencia de que en este caso la pesa reduce la presión en lugar de aumentarla. Tenemos inicialmente un cilindro que contiene un gas con presión volumen y temperatura:

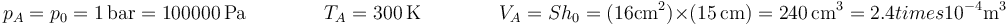
p_A = p_0=1\,\mathrm{bar} = 100000\,\mathrm{Pa}\qquad\qquad T_A = 300\,\mathrm{K}\qquad\qquad V_A = S h_0 = (16\mathrm{cm}^2)\times(15\,\mathrm{cm})=240\,\mathrm{cm}^3=2.4ºtimes 10^{-4}\mathrm{m}^3

Cuando se cuelga el saco, la presión externa se reduce en la cantidad correspondiente al peso

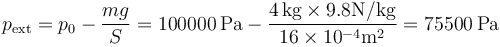
p_\mathrm{ext} = p_0-\frac{mg}{S}= 100000\,\mathrm{Pa}-\frac{4\,\mathrm{kg}\times 9.8\mathrm{N}/\mathrm{kg}}{16\times 10^{-4}\mathrm{m}^2}=75500\,\mathrm{Pa}

El nuevo estado de equilibrio se alcanza cuando la presión interior iguala a la nueva presión externa, siendo la temperatura final igual a la inicial, por no estar el sistema aislado térmicamente.

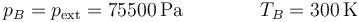
p_B = p_\mathrm{ext}=75500\,\mathrm{Pa}\qquad\qquad T_B = 300\,\mathrm{K}

Aplicando la ley de Boyle obtenemos el nuevo volumen

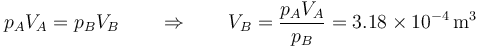
p_AV_A=p_BV_B\qquad\Rightarrow\qquad V_B = \frac{p_AV_A}{p_B}=3.18\times 10^{-4}\,\mathrm{m}^3

y la nueva distancia del pistón, dividiendo por la sección del tubo

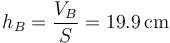
h_B = \frac{V_B}{S}= 19.9\,\mathrm{cm}

con lo que el descenso del pistón vale

\Delta h =h_B-h_A=4.9\,\mathrm{cm}\simeq 5\,\mathrm{cm}

3 Calor en el descenso

4 Calor en el ascenso

5 Producción de entropía

Obtenido de "http://tesla.us.es/wiki/index.php/Calor_en_una_expansi%C3%B3n_isoterma_por_un_peso"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace