Entrar Página Discusión Historial Go to the site toolbox

No Boletín - Cuestión sobre integral primera (Ex.Ene/13)

De Laplace

Contenido

1 Enunciado

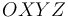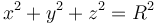En el sistema de referencia OXYZ\, de la figura, la partícula P\, se mueve bajo la acción de su propio peso y vinculada sin rozamiento a una superficie esférica fija de radio R\, y centro en el punto O\, (la ecuación de ligadura es x^{2}+y^{2}+z^{2}=R^{2}\,).

¿Cuál de las siguientes magnitudes físicas de la partícula P\, se conserva necesariamente constante durante el movimiento? (NOTA: sólo una de las cuatro opciones es correcta).

(a) La componente-z\, de su momento cinético respecto al punto O\,

(b) Su cantidad de movimiento

(c) Su energía cinética

(d) Su momento cinético respecto al punto O\,

2 Solución

Para saber cuál de las cuatro magnitudes propuestas es la que se conserva constante a lo largo del tiempo (integral primera), debemos examinar, en primer lugar, qué fuerzas actúan sobre la partícula y las características de las mismas. Y, después, habremos de ir revisando los teoremas de conservación asociados a las magnitudes propuestas hasta detectar cuál de ellos ve sus requisitos satisfechos en el caso que nos ocupa.

Las fuerzas que actúan sobre la partícula son dos: el peso (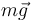m\vec{g}\,) y la fuerza de reacción vincular (\vec{\Phi}\,) ejercida por la superficie esférica.

El peso es una fuerza activa y, como tal, conocida a priori:

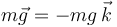
m\vec{g}=-mg\,\vec{k}

Sabemos, además, que el peso es una fuerza conservativa, y que va a realizar trabajo sobre la partícula porque en general la coordenada-z\, de ésta no va a permanecer constante durante su movimiento.

En cuanto a la fuerza de reacción vincular \vec{\Phi}\,, no conocemos a priori su módulo ni su sentido, pero sabemos que su dirección ha de ser perpendicular a la superficie esférica (al ser ésta un vínculo liso o sin rozamiento) y, por tanto, es radial:

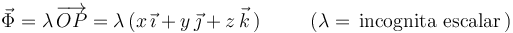
\vec{\Phi}=\lambda\,\overrightarrow{OP}=\lambda\,(x\,\vec{\imath}+y\,\vec{\jmath}+z\,\vec{k}\,)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(}\lambda=\,\mathrm{incognita}\,\,\mathrm{escalar}\,\mathrm{)}

También sabemos que \vec{\Phi}\, es una fuerza que no va a realizar trabajo, ya que el vínculo -además de liso- es esclerónomo o fijo y, por tanto, la trayectoria de la partícula va a ser siempre perpendicular a \vec{\Phi}\,. En efecto:

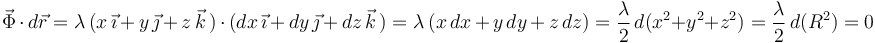
\vec{\Phi}\,\cdot\,d\vec{r}=\lambda\,(x\,\vec{\imath}\,+\,y\,\vec{\jmath}\,+\,z\,\vec{k}\,)\,\cdot\,(dx\,\vec{\imath}\,+\,dy\,\vec{\jmath}\,+\,dz\,\vec{k}\,)=\lambda\,(x\, dx\,+\,y\, dy\,+\,z\, dz)=\frac{\lambda}{2}\,d(x^{2}+y^{2}+z^{2})=\frac{\lambda}{2}\,d(R^{2})=0

3 Descartando la opción (b)

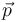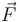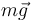Según el correspondiente teorema de conservación, la cantidad de movimiento \vec{p}\, de la partícula se conservaría constante si y sólo si la fuerza neta \vec{F}\, sobre la partícula fuese nula. Pero esto no ocurre aquí, ya que \vec{\Phi}\,, con su dirección radial, y m\vec{g}\,, con su dirección vertical, no pueden en general cancelarse mutuamente. En efecto:

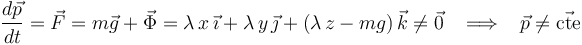
\frac{d\vec{p}}{dt}=\vec{F}=m\vec{g}+\vec{\Phi}=\lambda\,x\,\vec{\imath}+\lambda\,y\,\vec{\jmath}+(\lambda\,z-mg)\,\vec{k}\neq\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\, \vec{p}\neq\vec{\mathrm{cte}}

Nota: Obsérvese que, dada una posición arbitraria de la partícula sobre la esfera, no existe ninguna solución en 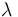\lambda\, para la cual se anulen simultánemente las tres componentes de \vec{F}\,.

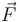4 Descartando la opción (c)

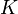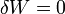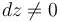Según el correspondiente teorema de conservación, para que se conservase constante la energía cinética K\, de la partícula sería necesario y suficiente que no se realizase trabajo neto sobre la partícula (\delta W=0\,). Sin embargo, en el caso que nos ocupa, si bien es cierto que \vec{\Phi}\, no trabaja, el peso sí que lo hace puesto que la coordenada-z\, de la partícula es variable (dz\neq 0\,). En efecto:

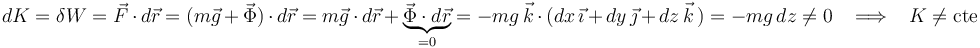
dK=\delta W=\vec{F}\,\cdot\, d\vec{r}=(m\vec{g}\,+\,\vec{\Phi})\,\cdot\, d\vec{r}=m\vec{g}\,\cdot\, d\vec{r}\,+\,\underbrace{\vec{\Phi}\cdot d\vec{r}}_{=0}=-mg\,\vec{k}\,\cdot\,(dx\,\vec{\imath}\,+\,dy\,\vec{\jmath}\,+\,dz\,\vec{k}\,)=-mg\,dz\neq 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,K\neq\mathrm{cte}

5 Descartando la opción (d)

El teorema de conservación del momento cinético 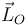\vec{L}_O\, de una partícula respecto al punto O\, establece que dicha magnitud se conserva constante en el tiempo si y sólo si es nulo el momento resultante respecto a O\, de las fuerzas actuantes sobre la partícula. En el caso que nos ocupa, si bien \vec{\Phi}\, tiene momento nulo respecto a O\, por tener dirección radial, no ocurre lo mismo con el peso, el cual sí que genera un momento (de fuerza) no nulo respecto a O\,. En efecto:

\frac{d\vec{L}_O}{dt}=\vec{M}_O=\overrightarrow{OP}\times \vec{F}=\overrightarrow{OP}\times (-mg\,\vec{k})+\underbrace{\overrightarrow{OP}\times\lambda\,\overrightarrow{OP}}_{=\vec{0}}=mg(-y\,\vec{\imath}+x\,\vec{\jmath}\,)\neq\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\, \vec{L}_O\neq\vec{\mathrm{cte}}

6 Eligiendo la opción (a)

Descartadas ya tres opciones, sólo resta comprobar que la opción (a) es la correcta. ¿Qué exige el teorema de conservación de una componente de momento cinético? Respuesta: la nulidad de la componente homóloga del momento resultante de fuerzas. Así que, si se trata de verificar la conservación de la componente-z\, del momento cinético de la partícula respecto al punto O\,, lo que hay que comprobar es la nulidad de la componente-z\, del momento resultante de fuerzas respecto a dicho punto.

Ya hemos comentado anteriormente que la única fuerza que genera momento respecto al punto O\, es el peso. Ahora bien, dicho momento del peso tiene nula su componente-z\, puesto que el propio peso tiene dirección paralela a OZ\,:

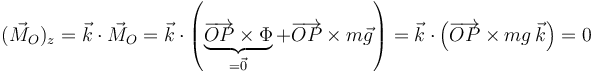
(\vec{M}_O)_z=\vec{k}\cdot\vec{M}_O=\vec{k}\cdot\left(\underbrace{\overrightarrow{OP}\times\Phi}_{=\vec{0}}+\overrightarrow{OP}\times m\vec{g}\right)=\vec{k}\cdot\left(\overrightarrow{OP}\times mg\,\vec{k}\right)=0

Queda confirmado, por tanto, que la opción correcta es la (a), ya que -conforme al teorema de conservación de una componente del momento cinético- sabemos que:

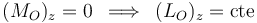
(M_O)_z=0\,\,\,\Longrightarrow\,\,\,(L_O)_z=\mathrm{cte}

7 Conservación de la energía mecánica

De lo hasta aquí dicho, ya podemos deducir una integral primera: la energía mecánica de la partícula (cinética más potencial). Porque se da la condición establecida por el correspondiente teorema de conservación: que todas las fuerzas que trabajen sobre la partícula sean conservativas (aquí sólo trabaja el peso, que es conservativo). Pero... miramos las cuatro opciones ofrecidas en el enunciado y resulta que la energía mecánica no es ninguna de ellas. Así que no nos queda otro remedio que seguir buscando otra integral primera.

Obtenido de "http://tesla.us.es/wiki/index.php/No_Bolet%C3%ADn_-_Cuesti%C3%B3n_sobre_integral_primera_(Ex.Ene/13)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace