No Boletín - Ley de Poiseuille (Ex.Ene/13)
De Laplace
1 Enunciado
Considérese un tubo cilíndrico, de radio  y longitud
y longitud  , a lo largo del cual fluye un cierto líquido. Bajo
ciertas condiciones, el volumen
, a lo largo del cual fluye un cierto líquido. Bajo
ciertas condiciones, el volumen 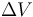 de líquido que pasa por el tubo en un intervalo de tiempo
de líquido que pasa por el tubo en un intervalo de tiempo 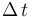 viene dado por la fórmula:
viene dado por la fórmula:
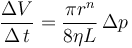
donde 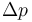 es la diferencia de presión entre los extremos del tubo, y
es la diferencia de presión entre los extremos del tubo, y 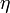 es la viscosidad dinámica del líquido (la unidad de
es la viscosidad dinámica del líquido (la unidad de 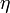 en el SI es
en el SI es 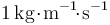 ).
¿Cuál es necesariamente el valor del exponente
).
¿Cuál es necesariamente el valor del exponente 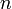 del radio tubular en la fórmula anterior?
del radio tubular en la fórmula anterior?
2 Solución
Para responder esta cuestión, basta con exigir homogeneidad dimensional a la fórmula que se nos ha dado en el enunciado. Al tomar dimensiones en ella, desaparecen del segundo miembro los factores numéricos "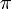 " (en el numerador) y "8" (en el denominador) por ser adimensionales, y se obtiene:
" (en el numerador) y "8" (en el denominador) por ser adimensionales, y se obtiene:
![\frac{[\Delta V]}{[\Delta\, t\,]}=\frac{[r\,]^{n}}{[\eta\,][L\,]}\,[\Delta p\,]](/wiki/images/math/b/d/4/bd4157e374fc8a277c1b507f80b0e502.png)
Observamos primero que algunas de las magnitudes presentes en la fórmula son magnitudes básicas. Es el caso del radio tubular  (longitud), de la longitud tubular
(longitud), de la longitud tubular  (longitud) y del intervalo de tiempo
(longitud) y del intervalo de tiempo 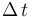 (tiempo).
(tiempo).
Hay un segundo grupo de magnitudes que son magnitudes derivadas pero de cuyas dimensiones el enunciado no nos informa. Se considera que debemos conocerlas, bien por su sencillez o bien por haber aparecido en otros ejercicios de boletín hechos en clase. Es el caso del volumen 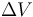 (longitud al cubo) y de la diferencia de presión
(longitud al cubo) y de la diferencia de presión 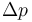 (fuerza partido por superficie):
(fuerza partido por superficie):
![[\Delta V]=L^3\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,[\Delta p\,]=\frac{[F\,]}{[S\,]}=\frac{MLT^{-2}}{L^2}=ML^{-1}T^{-2}](/wiki/images/math/0/6/3/06322d362f85c206d7f4d9f81dd5bb3d.png)
Sin embargo, sí que nos dice el enunciado cuál es la unidad SI de la viscosidad dinámica 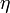 , lo cual nos permite deducir cuáles son las dimensiones de dicha magnitud:
, lo cual nos permite deducir cuáles son las dimensiones de dicha magnitud:
![\mathrm{unidad}\,\,\mathrm{SI}\,\,\mathrm{de}\,\, \eta = 1\,\mathrm{kg}\!\cdot\!\mathrm{m}^{-1}\!\!\cdot\!\mathrm{s}^{-1}\,\,\,\,\,\, \Longrightarrow \,\,\,\,\,\,[\eta\,]=ML^{-1}T^{-1}](/wiki/images/math/1/0/4/104561e10c5484235bea6d2ccce3bae5.png)
Sustituyendo, pues, las dimensiones de todas las magnitudes en la ecuación de homogeneidad dimensional, se obtiene:
![\frac{[\Delta V]}{[\Delta\, t\,]}=\frac{[r\,]^{n}}{[\eta\,][L\,]}\,[\Delta p\,]\,\,\,\,\,\Longrightarrow\,\,\,\,\,
\frac{L^3}{T}=\frac{L^{\, n}}{ML^{-1}T^{-1}L}\,ML^{-1}T^{-2}\,\,\,\,\,\Longrightarrow\,\,\,\,\,
L^3T^{-1}=L^{\, n-1}T^{-1}\,\,\,\,\,\Longrightarrow\,\,\,\,\, 3=n-1 \,\,\,\,\,\Longrightarrow\,\,\,\,\, n=4](/wiki/images/math/3/4/8/348aa5e0f2d9be045ee3f50ff9601812.png)





