No Boletín - Partícula en semicircunferencia (Ex.Dic/12)
De Laplace
Contenido |
1 Enunciado
En el plano vertical  (gravedad:
(gravedad: 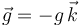 ), se halla una partícula
), se halla una partícula  , de masa
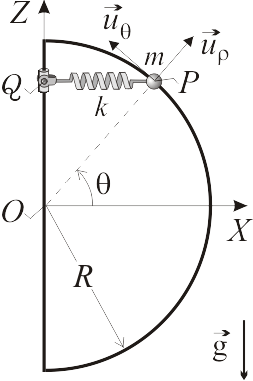
, de masa 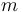 , ensartada sin rozamiento en la semicircunferencia fija, de radio
, ensartada sin rozamiento en la semicircunferencia fija, de radio  , que se muestra en la figura. Dicha partícula es solicitada desde el eje
, que se muestra en la figura. Dicha partícula es solicitada desde el eje  por un resorte elástico
por un resorte elástico 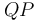 , de constante recuperadora
, de constante recuperadora 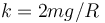 y longitud natural nula. El extremo
y longitud natural nula. El extremo  se puede desplazar sobre el eje
se puede desplazar sobre el eje  , de tal modo que el resorte permanece en todo instante paralelo al eje
, de tal modo que el resorte permanece en todo instante paralelo al eje  .
.
Utilizando la coordenada acimutal  para describir la posición de la partícula, y la base polar
para describir la posición de la partícula, y la base polar 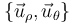 para expresar las magnitudes vectoriales, se pide:
para expresar las magnitudes vectoriales, se pide:
- Determinar la posición de equilibrio existente en el intervalo
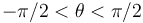 , así como la fuerza de reacción vincular que soportaría la partícula si se hallase en equilibrio en dicha posición.
, así como la fuerza de reacción vincular que soportaría la partícula si se hallase en equilibrio en dicha posición.
- Expresar la energía potencial de la partícula como una función de
 , y discutir si la posición de equilibrio del apartado anterior es estable o inestable.
, y discutir si la posición de equilibrio del apartado anterior es estable o inestable.
- Deducir razonadamente (mediante algún teorema de conservación) una integral primera del movimiento de la partícula, expresarla como una función de
 y
y 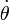 , y determinar su valor constante para el caso en que las condiciones iniciales sean:
, y determinar su valor constante para el caso en que las condiciones iniciales sean: 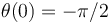 ,
, 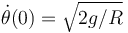 .
.
2 Posición de equilibrio y fuerza de reacción vincular
Sobre la partícula  actúan tres fuerzas: dos de naturaleza activa (su peso
actúan tres fuerzas: dos de naturaleza activa (su peso 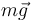 y la fuerza elástica
y la fuerza elástica 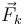 ejercida por el resorte) y una de reacción vincular (la fuerza
ejercida por el resorte) y una de reacción vincular (la fuerza  ejercida por la semicircunferencia). Dado que el vínculo es liso (sin rozamiento),
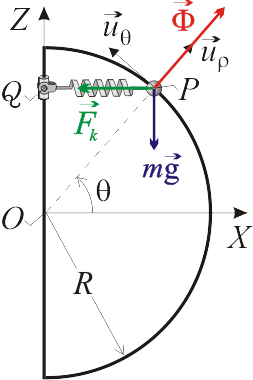
ejercida por la semicircunferencia). Dado que el vínculo es liso (sin rozamiento),  es perpendicular al propio vínculo y, por tanto, tiene dirección radial. En la figura adjunta se muestra el diagrama de las fuerzas, cuyas expresiones analíticas en la base polar son las siguientes:
es perpendicular al propio vínculo y, por tanto, tiene dirección radial. En la figura adjunta se muestra el diagrama de las fuerzas, cuyas expresiones analíticas en la base polar son las siguientes:
![\left\{\begin{array}{l} m\vec{g}=-mg\,[\mathrm{sen}(\theta)\,\vec{u}_{\rho}+\mathrm{cos}(\theta)\,\vec{u}_{\theta}] \\ \\ \vec{F}_k=-k\,\overrightarrow{QP}=-\displaystyle\frac{2\,mg}{R}R\,\mathrm{cos}(\theta)\,[\mathrm{cos}(\theta)\,\vec{u}_{\rho}-\mathrm{sen}(\theta)\,\vec{u}_{\theta}]=-2\,mg\,[\mathrm{cos}^2(\theta)\,\vec{u}_{\rho}-\mathrm{sen}(\theta)\mathrm{cos}(\theta)\,\vec{u}_{\theta}] \\ \\ \vec{\Phi}=\Phi\,\vec{u}_{\rho} \end{array}\right.](/wiki/images/math/5/f/d/5fd83a061b64cd6871f15e4f9999b9db.png)
Exigimos la condición de equilibrio: 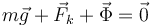
y la proyectamos sobre las direcciones radial y acimutal, obteniendo dos ecuaciones escalares:
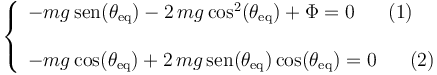
La ecuación (2) nos permite determinar las posiciones de equilibrio:
![mg\,\mathrm{cos}(\theta_{\mathrm{eq}})\,[-1+2\,\mathrm{sen}(\theta_{\mathrm{eq}})]=0\,\,\,\Longrightarrow\,\,\,
\left\{\begin{array}{l} \mathrm{cos}(\theta_{\mathrm{eq}})=0\,\,\,\Longrightarrow\,\,\,\mathrm{sin}\,\,\mathrm{solucion}\,\,\mathrm{en}\,\,\mathrm{el}\,\,\mathrm{intervalo}\,\, -\displaystyle\frac{\pi}{2}<\theta_{\mathrm{eq}}<\displaystyle\frac{\pi}{2} \\ \\ -1+2\,\mathrm{sen}(\theta_{\mathrm{eq}})=0\,\,\,\Longrightarrow\,\,\,\theta_{\mathrm{eq}}=\displaystyle\frac{\pi}{6}\,\mathrm{rad} \end{array}\right.](/wiki/images/math/0/4/3/043837aab0ae672539aba5b6d85b95e9.png)
La fuerza de reacción vincular en la posición de equilibrio se obtiene despejando 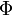 en la ecuación (1) y sustituyendo
en la ecuación (1) y sustituyendo 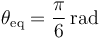 :
:
![\Phi=mg\,[\mathrm{sen}(\theta_{\mathrm{eq}})+2\,\mathrm{cos}^2(\theta_{\mathrm{eq}})]=2\,mg \,\,\,\Longrightarrow\,\,\,\vec{\Phi}=2\,mg \,\vec{u}_{\rho}](/wiki/images/math/e/4/6/e46460a3543a85ce751494d24b291919.png)
3 Energía potencial y discusión de la estabilidad/inestabilidad del equilibrio
Tanto el peso como la fuerza elástica son fuerzas conservativas. Por tanto, la energía potencial de la partícula es la suma de sus energías potenciales gravitatoria 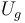 y elástica
y elástica 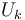 :
:
![U=U_g+U_k=mgz+\frac{1}{2}k|\overrightarrow{QP}|^2=mgR\,\mathrm{sen}(\theta)+\frac{1}{2}\,\frac{2mg}{R}\,[R\,\mathrm{cos}(\theta)]^2=mgR\,[\mathrm{sen}(\theta)+\mathrm{cos}^2(\theta)]](/wiki/images/math/b/c/1/bc1bfadda62b24097fefbb3e7553d2df.png)
Nótese que las expresiones propuestas para 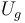 y
y 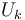 corresponden a tomar sus respectivos orígenes en
corresponden a tomar sus respectivos orígenes en 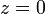 y
y 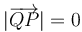 . Asimismo, obsérvese cómo la expresión final a la que se ha reducido la energía potencial pone de manifiesto que ésta depende exclusivamente de la posición de la partícula (definida mediante
. Asimismo, obsérvese cómo la expresión final a la que se ha reducido la energía potencial pone de manifiesto que ésta depende exclusivamente de la posición de la partícula (definida mediante  ).
).
La posición de equilibrio de la partícula podría haberse obtenido de forma alternativa calculando los extremos (máximos o mínimos) de la función energía potencial 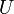 . Para ello, se iguala a cero la primera derivada de la función respecto a su variable:
. Para ello, se iguala a cero la primera derivada de la función respecto a su variable:
![\left.\frac{dU}{d\theta}\right|_{\theta=\theta_{\mathrm{eq}}}=mgR\,\mathrm{cos}(\theta_{\mathrm{eq}})[1-2\,\mathrm{sen}(\theta_{\mathrm{eq}})]=0](/wiki/images/math/5/b/8/5b873fec5117a3e18a5643dae558c80c.png)
Como vimos en el apartado anterior, la única solución de equilibrio en el intervalo definido por el enunciado es 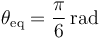 . Que dicha posición de equilibrio sea estable o inestable depende de si el extremo que la función
. Que dicha posición de equilibrio sea estable o inestable depende de si el extremo que la función 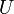 tiene en dicho punto es un mínimo o un máximo, respectivamente. Necesitamos, por tanto, evaluar en dicho punto la segunda derivada de
tiene en dicho punto es un mínimo o un máximo, respectivamente. Necesitamos, por tanto, evaluar en dicho punto la segunda derivada de 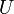 respecto a
respecto a  :
:
![\left.\frac{d^2U}{d\theta^2}\right|_{\theta=\frac{\pi}{6}}=-mgR\,[\mathrm{sen}(\theta)+2\,\mathrm{cos}(2\,\theta)]_{\theta=\frac{\pi}{6}}=-\frac{3}{2}mgR<0](/wiki/images/math/f/e/6/fe6fcdb1a7ddcdd7ee6d60973f179b61.png)
Al ser negativa la derivada segunda, se concluye que dicha posición de equilibrio corresponde a un máximo de energía potencial y, por tanto, se trata de una posición de equilibrio inestable.
4 Integral primera
La fuerza de reacción vincular  no trabaja sobre la partícula por ser siempre perpendicular a su desplazamiento (vínculo liso y esclerónomo). Así que todas las fuerzas que trabajan sobre la partícula (peso y elástica) son conservativas, y por tanto se conserva constante en el tiempo su energía mecánica
no trabaja sobre la partícula por ser siempre perpendicular a su desplazamiento (vínculo liso y esclerónomo). Así que todas las fuerzas que trabajan sobre la partícula (peso y elástica) son conservativas, y por tanto se conserva constante en el tiempo su energía mecánica 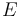 (suma de su energía cinética
(suma de su energía cinética 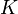 y su energía potencial
y su energía potencial 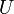 ). Dicho de otro modo, el teorema de conservación de la energía mecánica nos ha proporcionado la integral primera del movimiento de la partícula que nos pedía este apartado:
). Dicho de otro modo, el teorema de conservación de la energía mecánica nos ha proporcionado la integral primera del movimiento de la partícula que nos pedía este apartado: 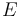 es una integral primera.
es una integral primera.
La velocidad de la partícula en la base polar viene dada en general por:
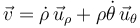
pero al particularizar para la trayectoria No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \rho=R\,\,\mathrm{(cte)}\,\,\,\Longrightarrow\,\,\,\dot{\rho}=0\,<\math>, queda: <center><math> \vec{v}=R\dot{\theta}\,\vec{u}_{\theta} </center> Así que la energía cinética de la partícula vale:
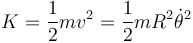
que sumada con la energía potencial (obtenida en el apartado anterior) nos da como resultado la energía mecánica de la partícula:
![E(\theta,\dot{\theta})=K+U=\frac{1}{2}mR^2\dot{\theta}^2+mgR\,[\mathrm{sen}(\theta)+\mathrm{cos}^2(\theta)]](/wiki/images/math/3/1/b/31b8a5067199d36f0adbc51ec498efbf.png)
El valor constante de esta integral primera se determina evaluando su expresión para las condiciones iniciales dadas 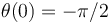 ,
, 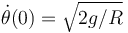 .
.
![E\left(-\frac{\pi}{2},\sqrt{\frac{2g}{R}}\right)=0 \,\,\,\Longrightarrow\,\,\,\frac{1}{2}mR^2\dot{\theta}^2+mgR\,[\mathrm{sen}(\theta)+\mathrm{cos}^2(\theta)]=0](/wiki/images/math/8/d/2/8d2e2cbfa6c2ca5bc2e365c64d4f9ef6.png)