No Boletín - Partícula en semicircunferencia (Ex.Dic/12)
De Laplace
Contenido |
1 Enunciado
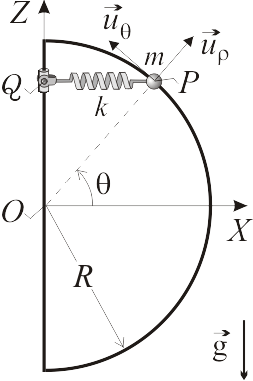
En el plano vertical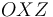 
(gravedad: 
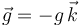), se halla una partícula 
, de masa 
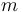, ensartada sin rozamiento en la semicircunferencia fija, de radio 
, que se muestra en la figura. Dicha partícula es solicitada desde el eje 
por un resorte elástico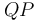 
, de constante recuperadora 
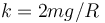y longitud natural nula. El extremo 
se puede desplazar sobre el eje , de tal modo que el resorte permanece en todo instante paralelo al eje 
.
Utilizando la coordenada acimutal 
para describir la posición de la partícula, y la base polar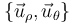 
para expresar las magnitudes vectoriales, se pide:
- Determinar la posición de equilibrio existente en el intervalo
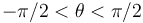, así como la fuerza de reacción vincular que soportaría la partícula si se hallase en equilibrio en dicha posición.
- Expresar la energía potencial de la partícula como una función de , y discutir si la posición de equilibrio del apartado anterior es estable o inestable.
- Deducir razonadamente (mediante algún teorema de conservación) una integral primera del movimiento de la partícula, expresarla como una función de y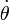
, y determinar su valor constante para el caso en que las condiciones iniciales sean: 
, 
.
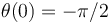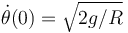2 Posición de equilibrio y fuerza de reacción vincular
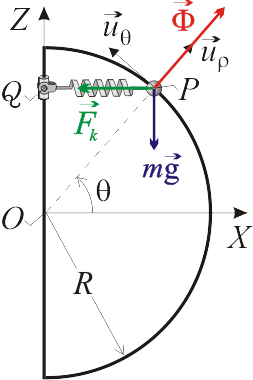
Sobre la partícula actúan tres fuerzas: dos de naturaleza activa (su peso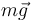 
y la fuerza elástica 
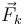ejercida por el resorte) y una de reacción vincular (la fuerza 
ejercida por la semicircunferencia). Dado que el vínculo es liso (sin rozamiento), es perpendicular al propio vínculo y, por tanto, tiene dirección radial. En la figura adjunta se muestra el diagrama de las fuerzas, cuyas expresiones analíticas en la base polar son las siguientes:
![\left\{\begin{array}{l} m\vec{g}=−mg\,[\mathrm{sen}(\theta)\,\vec{u}_{\rho}+\mathrm{cos}(\theta)\,\vec{u}_{\theta}] \\ \\ \vec{F}_k=-k\,\overrightarrow{QP}=-\displaystyle\frac{2mg}{R}R\,\mathrm{cos}(\theta)\,[\mathrm{cos}(\theta)\,\vec{u}_{\rho}-\mathrm{sen}(\theta)\,\vec{u}_{\theta}]=-2mg\,[\mathrm{cos}^2(\theta)\,\vec{u}_{\rho}-\mathrm{sen}(\theta)\mathrm{cos}(\theta)\,\vec{u}_{\theta}] \\ \\ \vec{\Phi}=\Phi\,\vec{u}_{\rho} \end{array}\right.](/wiki/images/math/0/1/b/01b77f7d0f19c62baf709d455ce0ef0f.png)
Exigimos la condición de equilibrio: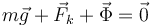 
y la proyectamos sobre las direcciones radial y acimutal, obteniendo dos ecuaciones escalares:
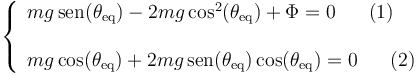
La ecuación (2) nos permite determinar las posiciones de equilibrio:
![mg\,\mathrm{cos}(\theta_{\mathrm{eq}})\,[−1+2\,\mathrm{sen}(\theta_{\mathrm{eq}})]=0\,\,\,\Longrightarrow\,\,\,
\left\{\begin{array}{l} \mathrm{cos}(\theta_{\mathrm{eq}})=0\,\,\,\Longrightarrow\,\,\,\mathrm{sin}\,\,\mathrm{solución}\,\,\mathrm{en}\,\,\mathrm{el}\,\,\mathrm{intervalo}\,\, -\displaystyle\frac{\pi}{2}<\theta_{\mathrm{eq}}<\displaystyle\frac{\pi}{2} \\ \\ −1+2\,\mathrm{sen}(\theta_{\mathrm{eq}})=0\,\,\,\Longrightarrow\,\,\,\theta_{\mathrm{eq}}=\displaystyle\frac{\pi}{6}\,\mathrm{rad} \end{array}\right.](/wiki/images/math/7/9/2/79259ea68b96b041dc0aea6613faad94.png)
