3.13. Partícula motorizada en aro (Ex.Ene/13)
De Laplace
Revisión a fecha de 12:59 20 feb 2013; Enrique (Discusión | contribuciones)
Enunciado
Una partícula 
, de masa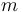 
, está ensartada sin rozamiento en un aro fijo de radio 
, el cual se halla situado en el plano horizontal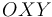 
y tiene su centro en el origen de coordenadas 
. Un motor ejerce una fuerza tangencial sobre la partícula, y como resultado ésta se mueve en sentido antihorario con una velocidad angular (escalar) que es función de la posición:
donde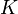 
es una constante positiva conocida, y el ángulo 
(definido en la figura) es el parámetro utilizado para describir la posición de la partícula sobre el aro.
- Determine la aceleración angular en función de la posición. ¿Qué tipo de movimiento circular realiza la partícula?
- Halle las componentes intrínsecas de la aceleración lineal en función de la posición.
- Calcule el trabajo que realiza el motor sobre la partícula al moverse ésta desde
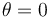hasta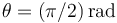 
.
- Determine la fuerza de reacción vincular ejercida por el aro sobre la partícula para la posición
.
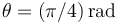