Entrar Página Discusión Historial Go to the site toolbox

Superposición de fuerzas electrostáticas (GIA)

De Laplace

1 Enunciado

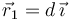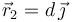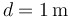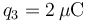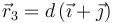Dos partículas con cargas eléctricas q1 = q2 = 1μC se encuentran situadas en las posiciones \vec{r}_1=d\!\ \vec{\imath} y \vec{r}_2=d\!\ \vec{\jmath}, siendo d=1\,\mathrm{m}. Se coloca una tercera partícula con carga q_3=2\,\mu\mathrm{C} en \vec{r}_3=d\!\ (\vec{\imath}+\vec{\jmath}).

  1. Calcular la fuerza sobre q3.
  2. ¿Qué valor ha de tener una carga q4 situada en el origen para que la fuerza neta sobre la partícula con carga q3 pase a ser nula?

2 Solución

2.1 Fuerza sobre la carga q3

Las fuerzas que describen la interacción electrostática verifican el principio de superposición. En el sistema que nos ocupa, la q3 está sometida a la acción simultánea de las cargas q1 y q2. La fuerza total 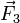\vec{F}_3 que actúa sobre aquélla es igual a la suma vectorial de las fuerzas electrostáticas que cada una de las cargas q1 y q2 ejercerían por separado, y que verificarán la ley de Coulomb:

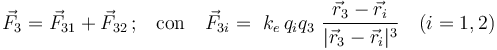
\vec{F}_3=\vec{F}_{31}+\vec{F}_{32}\,\mathrm{;}\quad\mbox{con}\quad\vec{F}_{3i}=\ k_e\!\ q_iq_3\ \frac{\vec{r}_3-\vec{r}_i}{|\vec{r}_3-\vec{r}_i|^3}\quad (i=1,2)

Utilizando las expresiones analíticas de los vectores que indican las posiciones de las tres cargas, se obtiene:

\vec{F}_3=\ k_e\!\ \frac{q_1q_3}{d^2}\ \vec{\jmath}+k_e\!\ \frac{q_2q_3}{d^2}\ \vec{\imath}=
Obtenido de "http://tesla.us.es/wiki/index.php/Superposici%C3%B3n_de_fuerzas_electrost%C3%A1ticas_(GIA)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace