Carga, potencial y energía de un campo dado
De Laplace
Contenido |
1 Enunciado
En el espacio vacío se ha detectado un campo electrostático con simetría esférica respecto de un punto fijo O, cuya función de campo viene dada por la expresi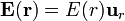ón 
, con
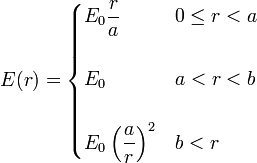
siendo r la distancia desde O al punto donde se evalúa el campo y E0, a y b$ son constantes conocidas.
- Determine cómo es la distribución de carga eléctrica que da lugar al campo descrito.
- Calcule la carga total de dicha distribución.
- Obtenga el valor del potencial eléctrico en O (
).
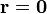- ¿Cuánto vale la energía electrostática del sistema?
2 Solución
2.1 Distribución de carga
La expresión del enunciado define un campo irrotacional en todos los puntos del espacio, pues al presentar simetría radial 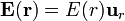se tendrá…
\begin{equation} \label{irrot} \nabla\times\mathbf{E}(\mathbf{r})=\frac{1}{r\sen\theta}\dpar{E(r)}{\varphi}\mathbf{u}_{\theta}- \frac{1}{r}\dpar{E(r)}{\theta}\mathbf{u}_{\varphi}=\mathbf{0}\ \mbox{;} \quad \forall \, P\in E_3 \end{equation} En consecuencia, dicho campo sólo tendrá fuentes escalares que, por tratarse de un campo eléctrico, serán cargas eléctricas. El objetivo de este apartado es determinar cómo están distribuidas dichas cargas, lo cuál están directamente relacionado con la forma del campo eléctrico.
\medskip
\noindent Como se sabe, en los puntos donde la función de campo presente una singularidad (el campo no toma un valor real) es porque hay una carga puntual $q_i$ o una distribución lineal de carga $\lambda(\mathbf{r})$. Una discontinuidad o salto en el valor del campo en los puntos de una superficie $\Sigma\subset E_3$ indica que en ésta existe una distribución superficial de carga eléctrica $\sigma_s(\mathbf{r})$ tal que\ldots \begin{equation} \label{sigma} \sigma_s(P)=\varepsilon_0\bn{\cdot}[\mathbf{E}]=\varepsilon_0\left( \mathbf{E}(P^+)-\mathbf{E}(P^-)\right)\cdot\bn\ \mbox{;}\quad \forall\, P\in\Sigma \end{equation} siendo $\bn$ el unitario normal a $\Sigma$ que apunta al semiespacio donde se halla $P^+$. Por otra parte, si en una región \mbox{\large $\tau$}$\subset E_3$ la función que define al campo eléctrico es continua y derivable se tendrá que, en general, existe una distribución volumétrica de carga eléctrica $\rho(\mathbf{r})$ que verifica\ldots \begin{equation} \label{rho} \rho(\mathbf{r})=\varepsilon_0\nabla \cdot \mathbf{E}(\mathbf{r})\ \mbox{;}\quad \forall\, P\in\mbox{\large $\tau$} \end{equation}
\noindent Las expresiones matemáticas que constituyen la función de campo toman valores reales en todos los puntos del espacio en que están definidas, por tanto no hay ni cargas puntuales ni distribuciones lineales de carga que actúen como fuentes de dicho campo eléctrico.
\smallskip
\noindent Como para $r=a^+$ y $r=a^-$, y para $r=b^+$ y $r=b^-$, el campo eléctrico se define de forma distinta, cabe la posibilidad de que en las superficies dados por $\Sigma_a:r=a\ $ y $\ \Sigma_b:r=b$ (superficies esféricas de radios $a$ y $b$, respectivamente, y centro en $O$) existan sendas distribuciones superficiales de carga eléctrica. Puesto que tanto $\Sigma_a$ como $\Sigma_b$ son superficies coordenadas en esféricas para $r$ constante, tendrán como vector normal $\bn=\mathbf{u}_{r}$, y aplicando (\ref{sigma}) se obtiene\ldots
\noindent En la superficie $\Sigma_a: r=a$ no hay carga eléctrica:
\[
\sigma_s(r=a)=\varepsilon_0
\left(\mathbf{E}(r=a^+)-\mathbf{E}(r=a^-)\right)\cdot\mathbf{u}_{r}
\quad\quad\Rightarrow\quad
\quad\fbox{$\displaystyle \sigma_s(\Sigma_a)
=\varepsilon_0\left(E_0-E_0\frac{a}{a}\right)=0$}
\]
En la superficie esférica $\Sigma_b: r=b\ $ la componente normal del
campo verifica una discontinuidad (la misma en todos los puntos); por
tanto, habrá carga eléctrica distribuida uniformemente:
\[
\sigma_s(r=b)=\varepsilon_0
\left(\mathbf{E}(r=b^+)-\mathbf{E}(r=b^-)\right)\cdot\mathbf{u}_{r}
\quad\quad\Rightarrow\quad
\quad\fbox{$\displaystyle \sigma_s(\Sigma_b)=
\varepsilon_0\left(E_0\left(\frac{a}{b}\right)^2-E_0\right)
=\varepsilon_0 E_0\ \frac{a^2-b^2}{b^2}<0$}
\]
\medskip
\noindent Estas superficies esféricas dividen el espacio en tres regiones, en cada una de las cuáles el campo eléctrico es continuo y derivable. Aplicando (\ref{rho}) en dichas regiones se obtiene cómo son las distribuciones volumétricas de carga:
\[ \rho(\mathbf{r})=\frac{\varepsilon_0}{r^2\sen\theta}\dpar{}{r}\bigg(r^2\sen\theta E(r)\bigg)\quad\Rightarrow\quad \rho(r) =\frac{\varepsilon_0}{r^2}\dtot{}{r}\big(r^2E(r)\big)=\cases{\displaystyle\frac{3\varepsilon_0 E_0}{a}=\rho_0\mbox{, cte.} \ ; & $0\leq r < a$ \cr & \cr \displaystyle\frac{2\varepsilon_0 E_0}{r}\ ; & $a< r < b$ \cr & \cr 0 \ ; & $b < r$} \] Es decir, en el interior de la esfera delimitada por la superficie $\Sigma_a$ la carga eléctrica se distribuye uniformemente; entre ésta y la superficie $\Sigma_b$ la densidad volumétrica de carga eléctrica es inversamente proporcional a la distancia al punto $O$, y fuera de la superficie $\Sigma_b$ no hay carga eléctrica.
