Carga, potencial y energía de un campo dado

De Laplace

1 Enunciado

En el espacio vacío se ha detectado un campo electrostático con simetría esférica respecto de un punto fijo O, cuya función de campo viene dada por la expresi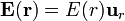ón , con

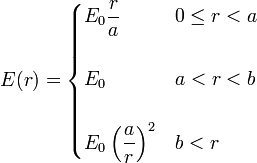
siendo r la distancia desde O al punto donde se evalúa el campo y E₀, a y b$ son constantes conocidas.

1. Determine cómo es la distribución de carga eléctrica que da lugar al campo descrito.
2. Calcule la carga total de dicha distribución.
3. Obtenga el valor del potencial eléctrico en O ().
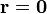4. ¿Cuánto vale la energía electrostática del sistema?

2 Solución

2.1 Distribución de carga

2.2 Carga total

2.3 Potencial eléctrico en el origen

2.4 Energía electrostática del sistema