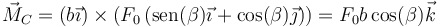Fuerza sobre una barra
De Laplace
Contenido |
1 Enunciado
Sobre una barra de longitud H y masa M situada en reposo horizontalmente en una superficie sin rozamiento se aplica una fuerza F0 también horizontal. El punto de la aplicación se encuentra a una distancia b del centro de la barra.
- Si la fuerza es perpendicular a la barra, ¿cuánto valen la aceleración del CM y la aceleración angular de la barra? ¿Alrededor de qué punto comienza a girar la barra?
- Suponga ahora que la fuerza forma un ángulo θ con la barra, ¿cuánto valen ese caso las aceleraciones y donde se encuentra el centro instantáneo de rotación?
- Suponga que la barra se encuentra articulada en un extremo de forma que sólo puede girar en torno a este punto. ¿Cuánto valen las aceleraciones en ese caso? ¿Cuánto vale la fuerza que el punto de articulación ejerce sobre la barra?
- Si la barra estuviera empotrada en su extremo, de forma que no pudiera moverse de ninguna manera, ¿cuánto valdrían la fuerza y el momento de reacción ejercidos por la articulación?
2 Aceleraciones
2.1 Aceleración lineal del centro de masas
La aceleración del centro de masas la calculamos aplicando el teorema de la cantidad de movimiento
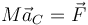
siendo  la resultante de todas las fuerzas externas aplicadas sobre el sólido. En nuestro caso, si situamos el origen de coordenadas en el centro de la barra y el eje OX a lo largo de ella, tenemos
la resultante de todas las fuerzas externas aplicadas sobre el sólido. En nuestro caso, si situamos el origen de coordenadas en el centro de la barra y el eje OX a lo largo de ella, tenemos
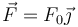
Técnicamente, a esta fuerza deberíamos añadir el peso de la barra y la reacción de la superficie horizontal, pero estas dos se anulan mutuamente.
Esto nos da la aceleración
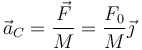
2.2 Aceleración angular
La aceleración angular del movimiento alrededor del CM la hallamos aplicando el teorema del momento cinético

siendo 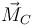 la resultante de los momentos de las diferentes fuerzas externas aplicadas
la resultante de los momentos de las diferentes fuerzas externas aplicadas
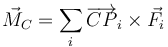
En nuestro caso tenemos el peso y la reacción normal, que son opuestas se aplican en el mismo punto y por tanto se cancelan, y el de la fuerza  , cuyo momento vale
, cuyo momento vale
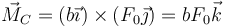
El momento de inercia respecto a un eje perpendicular a la varilla y que pasa por su centro de masas es
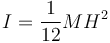
lo que nos da la aceleración angular
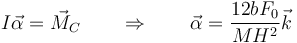
Esta aceleración angular se anula si b = 0, es decir, si empujamos la barra justamente en su centro, ésta no gira, solo se traslada.
2.3 Centro instantáneo de rotación
La barra no comienza a girar alrededor de su centro, ya que a la vez se está trasladando. Realiza un movimiento en el plano horizontal alrededor de un centro instantáneo de rotación, que será diferente en cada momento.
Puesto que parte del reposo, la velocidad del centro y la velocidad angular será en los primeros instantes

La posición del CIR respecto al centro de masas es
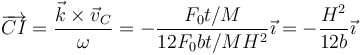
Este CIR se encuentra sobre la recta de la barra pero en un punto que depende de solamente de la longitud de la barra y del punto de aplicación. Nunca se halla en el propio centro de la barra, esto es, con una sola fuerza no podemos conseguir que la barra se limite a rotar sobre su centro; necesitamos un par de fuerzas para ello.
Para que empiece a girar alrededor de su extremo debe resultar una posición del CIR en
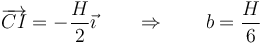
es decir, para conseguir que gire alrededor de un extremo no hay que empujarla en el otro, sino en un punto a 1/3 del otro extremo.
3 Fuerza oblicua
Cuando se aplica una fuerza oblicua, ya entra en juego el ángulo que aparece en el producto vectorial. La fuerza aplicada es ahora
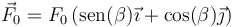
De aquí resulta una aceleración del Cm que es también oblicua
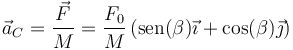
Para la aceleración angular, el nuevo momento de la fuerza vale