Entrar Página Discusión Historial Go to the site toolbox

Rodadura y deslizamiento de un disco

De Laplace

Contenido

1 Enunciado

Un disco de radio R y masa M rueda y desliza sobre el plano horizontal z = 0 de forma que la velocidad del punto de contacto con el suelo, A, y del diametralmente opuesto, B son de la forma

\vec{v}_A = v_A\vec{\imath}\qquad \vec{v}_B = v_B\vec{\imath}
  1. Calcule la velocidad angular del disco.
  2. Halle la velocidad del centro del disco, C, así como de los puntos D y E situados en los extremos de un diámetro horizontal.
  3. Determine la posición del centro instantáneo de rotación.
  4. Indique a qué se reducen los resultados anteriores en los casos particulares siguientes:
    1. vA = − vB
    2. vA = 0
    3. vA = vB

2 Introducción

Este es un movimiento sobre el plano XZ y por tanto, el estudio de la cinemática se reduce a dos dimensiones. Para todos los puntos del disco se cumplirá que

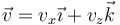
\vec{v}=v_x\vec{\imath}+v_z\vec{k}

con vx y vz las componentes cartesianas de la velocidad (que serán dependientes de la posición). Asimismo, la velocidad angular será perpendicular al plano del movimiento y por tanto irá en la dirección del eje OY

\vec{\omega}=\omega\vec{\jmath}

Esta velocidad angular es independiente de la posición (aunque variará en cada caso particular).

Al ser la velocidad angular ortogonal a las velocidades lineales, los movimientos posibles serán de reposo, traslación y rotación, pero nunca helicoidales.

3 Velocidad angular

POdemos hallar la velocidad angular a partir de la fórmula que relaciona las dos velocidades lineales

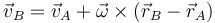
\vec{v}_B = \vec{v}_A+\vec{\omega}\times(\vec{r}_B-\vec{r}_A)

En este caso particular

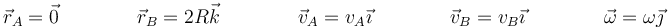
\vec{r}_A=\vec{0}\qquad\qquad\vec{r}_B=2R\vec{k}\qquad\qquad\vec{v}_A=v_A\vec{\imath}\qquad\qquad\vec{v}_B=v_B\vec{\imath}\qquad\qquad \vec{\omega}=\omega\vec{\jmath}

lo que nos da

v_B\vec{\imath}=v_A\vec{\imath}+(\omega\vec{\jmath})\times(2R\vec{k})=(v_A+2R\omega)\vec{\imath}

y despejando de aquí

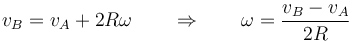
v_B = v_A +2R\omega\qquad\Rightarrow\qquad \omega =\frac{v_B-v_A}{2R}

Dependiendo de las magnitudes relativas de las velocidades lineales, esta velocidad angular puede ser positiva, negativa o nula. Si A se mueve más rápidamente que B, el giro es antihorario respecto al plano XZ (ω < 0), si A se mueve más lento, el giro es horario. Si tienen la misma velocidad, no hay giro alguno.

4 Velocidades lineales

Una vez que tenemos la velocidad de un punto (de dos, de hecho) y la velocidad angular podemos hallar la velocidad de cualquier otro, empleando la fórmula

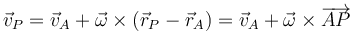
\vec{v}_P = \vec{v}_A+\vec{\omega}\times(\vec{r}_P-\vec{r}_A)=\vec{v}_A+\vec{\omega}\times\overrightarrow{AP}

4.1 Centro del disco

Respecto del punto A, la posición del centro del disco es

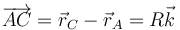
\overrightarrow{AC}=\vec{r}_C-\vec{r}_A=R\vec{k}

y obtenemos la velocidad del centro

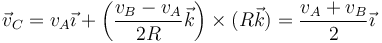
\vec{v}_C=v_A\vec{\imath}+\left(\frac{v_B-v_A}{2R}\vec{k}\right)\times(R\vec{k})=\frac{v_A+v_B}{2}\vec{\imath}

El resultado es que el centro del disco se mueve con una velocidad que es la media aritmética de las de los puntos diametralmente opuestos.

Una vez que tenemos la velocidad del centro del disco, podemos hallar la velocidad de cualquier otro punto también empleando la fórmula correspondiente

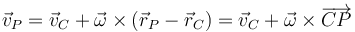
\vec{v}_P = \vec{v}_C+\vec{\omega}\times(\vec{r}_P-\vec{r}_C)=\vec{v}_C+\vec{\omega}\times\overrightarrow{CP}

4.2 Diámetro horizontal

La posición del punto D respecto al centro del disco es

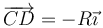
\overrightarrow{CD}=-R\vec{\imath}

por lo que su velocidad lineal vale

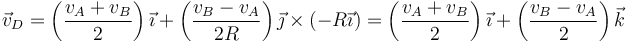
\vec{v}_D=\left(\frac{v_A+v_B}{2}\right)\vec{\imath}+\left(\frac{v_B-v_A}{2R}\right)\vec{\jmath}\times(-R\vec{\imath})= \left(\frac{v_A+v_B}{2}\right)\vec{\imath}+\left(\frac{v_B-v_A}{2}\right)\vec{k}

La ventaja de usar el punto C en vez del A como referencia es que el vector de posición relativo es un poco más simple, pero al mismo resultado se puede llegar empleando A en lugar de C.

Para el punto E, diametralmente opuesto al D, el cálculo es análogo

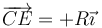
\overrightarrow{CE}=+R\vec{\imath}

resultando la velocidad

\vec{v}_E=\left(\frac{v_A+v_B}{2}\right)\vec{\imath}+\left(\frac{v_B-v_A}{2R}\right)\vec{\jmath}\times(+R\vec{\imath})= \left(\frac{v_A+v_B}{2}\right)\vec{\imath}-\left(\frac{v_B-v_A}{2}\right)\vec{k}

Estas dos velocidades tienen una componente horizontal de avance y una vertical que puede ser ascendente o descendente dependiendo de si la rapidez de A es mayor que la de B o viceversa.

5 Centro instantáneo de rotación

6 Casos particulares

6.1 vA = vB

6.2 vA = 0

6.3 vA = −vB

Obtenido de "http://tesla.us.es/wiki/index.php/Rodadura_y_deslizamiento_de_un_disco"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace