Entrar Página Discusión Historial Go to the site toolbox

Rodadura y deslizamiento de un disco

De Laplace

Contenido

1 Enunciado

Un disco de radio R y masa M rueda y desliza sobre el plano horizontal z = 0 de forma que la velocidad del punto de contacto con el suelo, A, y del diametralmente opuesto, B son de la forma

\vec{v}_A = v_A\vec{\imath}\qquad \vec{v}_B = v_B\vec{\imath}
  1. Calcule la velocidad angular del disco.
  2. Halle la velocidad del centro del disco, C, así como de los puntos D y E situados en los extremos de un diámetro horizontal.
  3. Determine la posición del centro instantáneo de rotación.
  4. Indique a qué se reducen los resultados anteriores en los casos particulares siguientes:
    1. vA = − vB
    2. vA = 0
    3. vA = vB

2 Introducción

Este es un movimiento sobre el plano XZ y por tanto, el estudio de la cinemática se reduce a dos dimensiones. Para todos los puntos del disco se cumplirá que

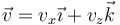
\vec{v}=v_x\vec{\imath}+v_z\vec{k}

con vx y vz las componentes cartesianas de la velocidad (que serán dependientes de la posición). Asimismo, la velocidad angular será perpendicular al plano del movimiento y por tanto irá en la dirección del eje OY

\vec{\omega}=\omega\vec{\jmath}

Esta velocidad angular es independiente de la posición (aunque variará en cada caso particular).

Al ser la velocidad angular ortogonal a las velocidades lineales, los movimientos posibles serán de reposo, traslación y rotación, pero nunca helicoidales.

3 Velocidad angular

POdemos hallar la velocidad angular a partir de la fórmula que relaciona las dos velocidades lineales

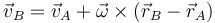
\vec{v}_B = \vec{v}_A+\vec{\omega}\times(\vec{r}_B-\vec{r}_A)

En este caso particular

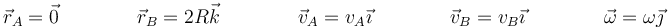
\vec{r}_A=\vec{0}\qquad\qquad\vec{r}_B=2R\vec{k}\qquad\qquad\vec{v}_A=v_A\vec{\imath}\qquad\qquad\vec{v}_B=v_B\vec{\imath}\qquad\qquad \vec{\omega}=\omega\vec{\jmath}

lo que nos da

v_B\vec{\imath}=v_A\vec{\imath}+(\omega\vec{\jmath})\times(2R\vec{k})=(v_A+2R\omega)\vec{\imath}

y despejando de aquí

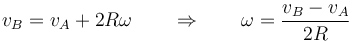
v_B = v_A +2R\omega\qquad\Rightarrow\qquad \omega =\frac{v_B-v_A}{2R}

Dependiendo de las magnitudes relativas de las velocidades lineales, esta velocidad angular puede ser positiva, negativa o nula. Si A se mueve más rápidamente que B, el giro es antihorario respecto al plano XZ (ω < 0), si A se mueve más lento, el giro es horario. Si tienen la misma velocidad, no hay giro alguno.

4 Velocidades lineales

5 Centro instantáneo de rotación

6 Casos particulares

6.1 vA = vB

6.2 vA = 0

6.3 vA = −vB

Obtenido de "http://tesla.us.es/wiki/index.php/Rodadura_y_deslizamiento_de_un_disco"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace