No Boletín - Composición de aceleraciones angulares (Ex.Ene/12)

De Laplace

Revisión a fecha de 11:27 1 dic 2012; Enrique (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Dados tres sólidos rígidos ("0", "1" y "2"), se conocen como funciones del tiempo las siguientes velocidades angulares:

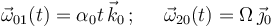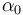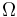$\vec{\omega}_{01}(t)=\alpha_0t\,\vec{k}_0\,;\,\,\,\,\,\,\,\,\vec{\omega}_{20}(t)=\Omega\,\vec{\jmath}_0$ ( $\alpha_0\,$ y $\Omega\,$ son constantes conocidas)

donde 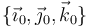$\{\vec{\imath}_0, \vec{\jmath}_0, \vec{k}_0\}\,$ es una base ortonormal que se mueve solidariamente con "0".

Determine la aceleración angular 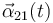$\vec{\alpha}_{21}(t)\,$

2 Solución

Calculamos, mediante su definición, las aceleraciones angulares de los movimientos {01} y {20}:

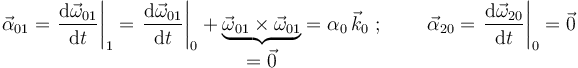
$\vec{\alpha}_{01}=\left.\frac{\mathrm{d}\vec{\omega}_{01}}{\mathrm{d}t}\right|_1=\left.\frac{\mathrm{d}\vec{\omega}_{01}}{\mathrm{d}t}\right|_0+\underbrace{\vec{\omega}_{01}\times\vec{\omega}_{01}}_{\displaystyle =\vec{0}}=\alpha_0\,\vec{k}_0\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{\alpha}_{20}=\left.\frac{\mathrm{d}\vec{\omega}_{20}}{\mathrm{d}t}\right|_0=\vec{0}$

y, a continuación, determinamos la aceleración angular del movimiento {21} mediante la ley de composición de aceleraciones angulares:

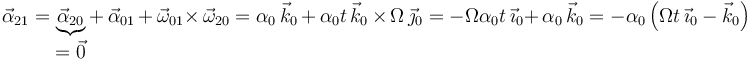
$\vec{\alpha}_{21}=\underbrace{\vec{\alpha}_{20}}_{\displaystyle =\vec{0}}+\,\vec{\alpha}_{01}\,+\,\vec{\omega}_{01}\times\,\vec{\omega}_{20}=\alpha_0\,\vec{k}_0\,+\,\alpha_0t\,\vec{k}_0\,\times\,\Omega\,\vec{\jmath}_0=-\Omega\alpha_0t\,\vec{\imath}_0+\,\alpha_0\,\vec{k}_0=-\alpha_0\left(\Omega t\,\vec{\imath}_0-\vec{k}_0\right)$

También se puede calcular la aceleración angular {21} derivando respecto al tiempo la velocidad angular {21} (previamente determinada por composición de velocidades angulares):

$\vec{\omega}_{21}=\vec{\omega}_{20}\,+\,\vec{\omega}_{01}=\Omega\,\vec{\jmath}_0\,+\,\alpha_0 t\,\vec{k}_0\,\,\,\longrightarrow\,\,\,\vec{\alpha}_{21}=\left.\frac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_1=\left.\frac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_0\,+\,\vec{\omega}_{01}\,\times\,\vec{\omega}_{21}=-\alpha_0\left(\Omega t\,\vec{\imath}_0-\vec{k}_0\right)$

No Boletín - Composición de aceleraciones angulares (Ex.Ene/12)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES