Entrar Página Discusión Historial Go to the site toolbox

Conservación de magnitudes en movimiento curvo

De Laplace

Contenido

1 Enunciado

Una partícula de masa m describe el movimiento plano

\rho = A\,\mathrm{sen}(\Omega t)\qquad\varphi = \Omega t\qquad\qquad\ t \in(0,\pi/\Omega)
  1. Calcule la fuerza que actúa sobre la partícula en cualquier instante del intervalo.
  2. Halle el impulso que experimenta entre t = 0 y t = π / (2Ω).
  3. Demuestre que el momento cinético de la partícula respecto al origen no se conserva, pero respecto al punto 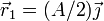\vec{r}_1 = (A/2)\vec{\jmath} sí.
  4. Calcule la energía cinética de la partícula. ¿Se conserva esta cantidad?

2 Fuerza

Podemos calcular la fuerza aplicando la segunda ley de Newton

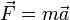
\vec{F}=m\vec{a}

que en coordenadas polares se escribe

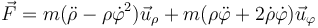
\vec{F}=m(\ddot{\rho}-\rho\dot{\varphi}^2)\vec{u}_\rho+m(\rho\ddot{\varphi}+2\dot{\rho}\dot{\varphi})\vec{u}_{\varphi}

Las derivadas de las dos coordenadas valen

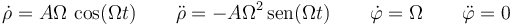
\dot{\rho}=A\Omega\,\cos(\Omega t)\qquad\ddot{\rho}=-A\Omega^2\,\mathrm{sen}(\Omega t)\qquad\dot{\varphi}=\Omega \qquad\ddot{\varphi}=0

lo que nos da la fuerza

\vec{F}=-2mA\Omega^2\mathrm{sen}(\Omega t)\vec{u}_\rho + 2mA\Omega^2\cos(\Omega t)\vec{u}_\varphi

3 Impulso

4 Momento cinético

5 Energía cinética

Obtenido de "http://tesla.us.es/wiki/index.php/Conservaci%C3%B3n_de_magnitudes_en_movimiento_curvo"

Herramientas:

TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace