Cantidad de movimiento y momento cinético (GIE)

De Laplace

Revisión a fecha de 16:46 23 nov 2012; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Integrales primeras
2 Cantidad de movimiento
3 Momento cinético

1 Integrales primeras

Una constante de movimiento (también llamada integral primera) es una magnitud función de la posición, velocidad de la partícula (o de las partículas, si hay más de una) cuyo valor es constante, pese a que la posición y la velocidad sí son variables en el tiempo

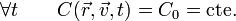
$\forall t\qquad C(\vec{r},\vec{v},t)=C_0=\mathrm{cte.}$

Por ejemplo, supongamos una partícula que describe el movimiento circular

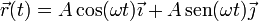
$\vec{r}(t) = A\cos(\omega t)\vec{\imath}+A\,\mathrm{sen}(\omega t)\vec{\jmath}$

Este movimiento verifica las relaciones

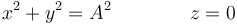
$x^2 + y^2 = A^2\qquad\qquad z=0$

Así, aunque tanto $x$ como $y$ son funciones del tiempo, una combinación de las dos coordenadas permanece constante. Si hubiéramos conocido esta constancia antes de determinar la ley horaria, sabríamos que la trayectoria es una circunferencia, aunque la rapidez pudiera ser desconocida.

El valor concreto de una constante de movimiento puede calcularse a partir de las condiciones iniciales (o de los valores de la posición y velocidad en cualquier instante)

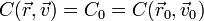
$C(\vec{r},\vec{v})=C_0=C(\vec{r}_0,\vec{v}_0)\,$

El ejemplo más conocido de constante de movimiento, que veremos más adelante, es el de la energía mecánica. Cuando un cuerpo cae, su posición varía y su velocidad aumenta, pero la energía mecánica, que es una cierta combinación de la posición y la velocidad, permanece constante.

Las integrales primeras pueden tener una interpretación física directa (como la energía o el momento cinético) o ser combinaciones más o menos abstractas válidas para un solo problema concreto. A continuación estudiaremos tres magnitudes, construidas a partir de la posición y la velocidad, cuyas leyes de evolución pueden determinarse a partir de las leyes de Newton. Estas cantidades, si se dan las condiciones adecuadas, son candidatas a ser constantes de movimiento, y por tanto son las primeras candidatas cuando en un problema se buscan integrales primeras. Estas magnitudes son:

La cantidad de movimiento
El momento cinético
La energía (cinética, potencial y mecánica).

2 Cantidad de movimiento

2.1 Definición

Se define la cantidad de movimiento de una partícula como el producto de su masa por su velocidad

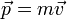
$\vec{p}=m\vec{v}\,$

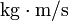Sus dimensiones son $M L T - 1$ y sus unidades en el SI son $\mathrm{N}\cdot\mathrm{s}$ (o $\mathrm{kg}\cdot\mathrm{m}/\mathrm{s}$ )

2.2 Teorema de la cantidad de movimiento

A partir de la definición es inmediato que

$\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}=m\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=m\vec{a} = \vec{F}$

esto es, la derivada respecto al tiempo de la cantidad de movimiento es igual a la resultante de las fuerzas aplicadas sobre la partícula.

2.3 Impulso

En ocasiones, no nos interesa tanto saber cómo cambia la cantidad de movimiento en un intervalo de tiempo infinitesimal, sino saber cuánto varía durante un cierto periodo. Supongamos una partícula que viaja libremente y por tanto con cantidad de movimiento constante 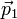$\vec{p}_1$ . Entonces es sometida a una fuerza 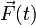$\vec{F}(t)$ durante un intervalo entre $t 1$ y $t 2$ (por ejemplo, durante una colisión, a partir del cual vuelve a moverse libremente, con cantidad de movimiento constante 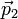$\vec{p}_2$ . Se trata de hallar el incremento en la cantidad de movimiento durante la colisión. Integrando en la segunda ley de Newton obtenemos

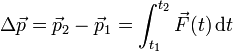
$\Delta \vec{p}=\vec{p}_2-\vec{p}_1 = \int_{t_1}^{t_2}\vec{F}(t)\,\mathrm{d}t$

Esta integral de la fuerza sobre un intervalo recibe el nombre de impulso, por lo que la igualdad anterior establece que

“El incremento de la cantidad de movimiento es igual al impulso recibido”

Esta relación, aparentemente trivial, tiene su importancia en la teoría de colisiones y de percusiones, donde se ignora el valor exacto de la fuerza, pero sí se conoce el valor del impulso.

Así, por ejemplo, en un saque de tenis, la rapidez de la pelota pasa de ser prácticamente nula a valer unos 60 m/s. Dado que la masa de una pelota es de 68 g, esto supone un impulso

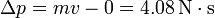
$\Delta p = m v - 0 = 4.08\,\mathrm{N}\cdot\mathrm{s}$

No conocemos la fuerza instantánea sobre la pelota, puesto que su deformación la convierte en un problema muy complejo. Podemos hallar la fuerza media, si conocemos el tiempo de colisión. Un valor típico podrían ser 30 ms, lo que nos da una fuerza media

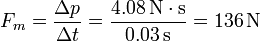
$F_m = \frac{\Delta p}{\Delta t} = \frac{4.08\,\mathrm{N}\cdot\mathrm{s}}{0.03\,\mathrm{s}}=136\,\mathrm{N}$

Por comparación, esta fuerza es 2000 veces el peso, o lo que es lo mismo, la pelota experimenta una aceleración de unos 200g.

2.4 Teorema de conservación

De la segunda ley de Newton es inmediato que:

“La cantidad de movimiento de una partícula permanece constante cuando la resultante de las fuerzas que actúan sobre ella es nula durante un intervalo de tiempo”

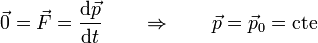
$\vec{0}=\vec{F} = \frac{\mathrm{d}\vec{p}}{\mathrm{d}t}\qquad\Rightarrow\qquad \vec{p}=\vec{p}_0=\mathrm{cte}$

Puesto que la masa de la partícula permanece constante, si la cantidad de movimiento se conserva, la velocidad también permanece constante

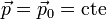
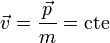
$\vec{p}=\vec{p}_0=\mathrm{cte}$ $\Rightarrow$ $\vec{v}=\frac{\vec{p}}{m}=\mathrm{cte}$

Por tanto, si la resultante de las fuerzas que actúan sobre la partícula se anula durante un intervalo de tiempo, la partícula se mueve uniformemente durante dicho periodo.

Esto no es exactamente lo mismo que lo que dice la Primera Ley de Newton, pues esta ley habla de partícula no sometida a ninguna interacción, mientras que el teorema de conservación se refiere a una partícula sometida a diferentes fuerzas, pero tales que su resultante es nula.

Para el caso de una partícula este teorema de conservación aporta poca información nueva. Sin embargo, su extensión al caso de un sistema de partículas es extremadamente útil.

3 Momento cinético

3.1 Definiciones

Momento cinético: Se define el momento cinético (o momento angular) de una partícula respecto a un punto fijo O como

$\vec{L}_O = \vec{r}\times\vec{p}=m\vec{r}\times\vec{v}$

siendo

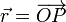
$\vec{r}=\overrightarrow{OP}$

el vector de posición del punto P relativa al punto O.

Momento de una fuerza: Se define el momento de una fuerza respecto a un punto fijo O como

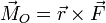
$\vec{M}_O = \vec{r}\times\vec{F}$

Si tenemos varias fuerzas actuando sobre la misma partícula, el momento resultante es igual al momento de la resultante

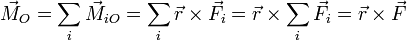
$\vec{M}_O=\sum_i \vec{M}_{iO}=\sum_i\vec{r}\times\vec{F}_i = \vec{r}\times\sum_i\vec{F}_i =\vec{r}\times\vec{F}$

3.2 Derivada del momento cinético (Teorema del momento cinético)

Como consecuencia de la segunda ley de Newton, la derivada del momento cinético de una partícula es igual al momento resultante sobre ella

$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t} =m\left(\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\right)\times\vec{v}+m\,\vec{r}\times\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=m\overbrace{\vec{v}\times\vec{v}}^{=\vec{0}}+\vec{r}\times\vec{F}=\vec{M}_O$

3.3 Teorema de conservación

De la expresión para la derivada del momento cinético se deduce su teorema de conservación:

Si la resultante de los momentos de las fuerzas que actúan sobre una partícula es nula, el momento cinético de dicha partícula permanece constante.

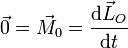
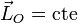
$\vec{0} = \vec{M}_0=\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}$ $\Rightarrow$ $\vec{L}_O=\mathrm{cte}$

3.4 Fuerzas centrales

Las fuerzas centrales constituyen un caso particular e importante de las diferentes fuerzas presentes en la naturaleza. Una fuerza central es aquella que en todos los puntos del espacio posee dirección radial desde un punto fijo O, siendo además dependiente solo de la distancia a dicho punto

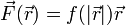
$\vec{F}(\vec{r}) = f(|\vec{r}|)\vec{r}$

Ejemplos de fuerzas centrales son la fuerza de la gravedad debida a un objeto masivo (como la atracción que el Sol ejerce sobre la Tierra), o la fuerza eléctrica debida a una carga en reposo.

Se tiene que

El momento cinético respecto a un punto O de una partícula sometida a la acción de una fuerza central, con centro O, permanece constante.

La demostración es inmediata, ya que el vector de posición relativo y la fuerza son vectores paralelos

$\vec{M}_O = \vec{r}\times\overbrace{\vec{F}}^{\parallel\vec{r}} = \vec{0}\qquad\Rightarrow\qquad \vec{L}_O = \mathrm{cte}$

Una consecuencia inmediata de la conservación del momento cinético para una fuerza central es:

La trayectoria de una partícula sometida a una fuerza central es plana.

El plano en el que ocurre la trayectoria es el definido por el centro de fuerzas, la posición inicial y la velocidad inicial.

Puesto que el momento cinético se conserva tenemos que si multiplicamos escalarmente el vector de posición relativo por este vector constante

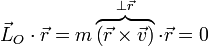
$\vec{L}_O\cdot\vec{r}=m\overbrace{\left(\vec{r}\times\vec{v}\right)}^{\perp\vec{r}}\cdot\vec{r} = 0$

Esta es la ecuación vectorial de un plano que pasa por O y es normal a la dirección de $\vec{L}_O$ .

Este resultado también es válido para fuerzas no centrales que conservan el momento cinético.

3.5 Conservación parcial del momento cinético

Existen ocasiones en que el momento cinético no se conserva. Sin embargo, incluso en esos casos es a menudo posible obtener una ley de conservación más restringida.

Para ello, tenemos en cuenta que el momento cinético es un vector y posee tres componentes. Puede ocurrir que aunque el vector como tal no sea constante, una de sus componentes sí lo sea. Sea $\vec{u}$ un vector unitario fijo. La componente del momento angular según la dirección de $\vec{u}$ es

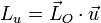
$L_{u}=\vec{L}_O\cdot\vec{u}\,$

Derivando aquí respecto al tiempo

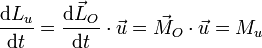
$\frac{\mathrm{d}L_u}{\mathrm{d}t}=\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\cdot\vec{u}=\vec{M}_O\cdot\vec{u}=M_u$

Si se anula la componente en la dirección de $\vec{u}$ del momento de las fuerzas aplicadas, la componente del momento cinético en dicha dirección permanece constante.

Cantidad de movimiento y momento cinético (GIE)

De Laplace

Contenido

1 Integrales primeras

2 Cantidad de movimiento

2.1 Definición

2.2 Teorema de la cantidad de movimiento

2.3 Impulso

2.4 Teorema de conservación

3 Momento cinético

3.1 Definiciones

3.2 Derivada del momento cinético (Teorema del momento cinético)

3.3 Teorema de conservación

3.4 Fuerzas centrales

3.5 Conservación parcial del momento cinético

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES