Barra articulada en otra barra, Noviembre 2012 (G.I.C.)
De Laplace
Revisión a fecha de 22:34 18 nov 2012; Pedro (Discusión | contribuciones)
1 Enunciado
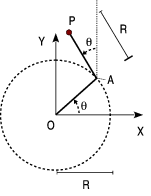
Una barra de radio R gira alrededor de uno de sus extremos, situado en el punto O. En su otro extremo se articula otra barra de longitud R que a su vez gira en con la misma velocidad angular.
- Expresa el vector de posición
 en función del ángulo θ de la figura.
en función del ángulo θ de la figura.
- Si
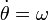 y el módulo de la velocidad del punto P es v0, encuentra el valor de ω.
y el módulo de la velocidad del punto P es v0, encuentra el valor de ω.
- Calcula el vector normal en cada punto de la trayectoria de P.
- Calcula la curvatura en cada punto de la trayectoria.
2 Solución
2.1 Vector de posición
El vector de posición del punto P puede construirse como la suma
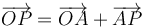
Tenemos

Por otro lado
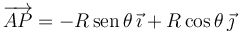
Por tanto el vector buscado es