Problemas de movimiento plano (G.I.T.I.)
De Laplace
1 Movimiento de un aro en un pasador
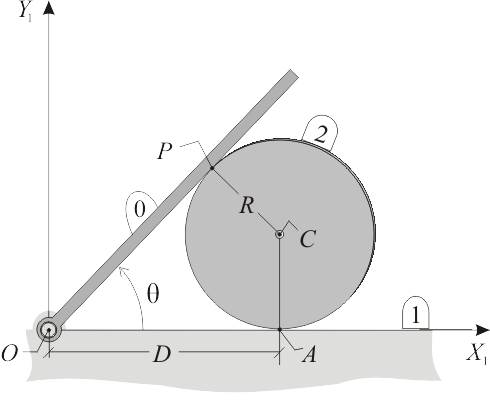
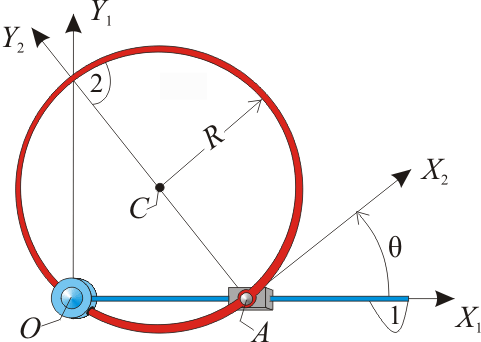
Sea un aro de centro C y radio R (sólido “2”) que se mueve, en un plano fijo OX1Y1 (sólido 1), de tal modo que está obligado a deslizar en todo instante por el interior de un pasador giratorio situado en el punto O, y además se halla articulado en su punto A a un deslizador que se mueve siempre sobre el eje horizontal OX1 (ver figura). Con carácter auxiliar, se define el sistema de ejes AX2Y2 (sólido 2) solidario con el aro en su movimiento.
- Determine gráfica y analíticamente la posición del C.I.R. del movimiento {21}.
- Sabiendo que el ángulo θ, que forman los ejes OX1 y AX2, verifica la ley horaria θ(t) = Ωt (donde Ω es una constante conocida), calcule
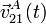 y
y 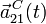 .
.
2 Movimiento de barra en un pasador
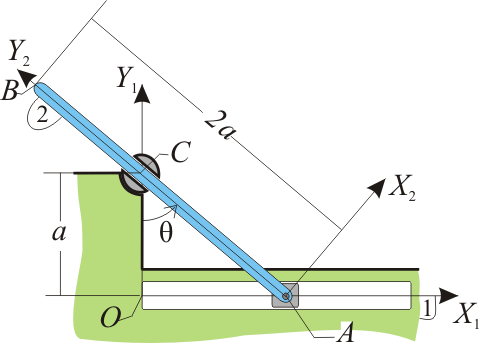
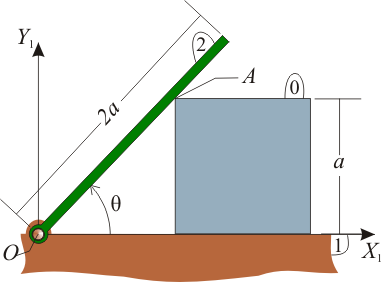
La barra AB (sólido “2”), de longitud 2a, puede deslizar en su extremo A por el eje OX1 de la escuadra fija OX1Y1 (sólido “1”), al mismo tiempo que desliza por el interior de un pasador orientable ubicado en el punto C del eje OY1, a una distancia a del origen O. Sabiendo que la barra gira con velocidad angular constante Ω (ley horaria θ(t) = Ωt, donde θ es el ángulo definido en la figura), se pide:
- Determinar gráficamente la posición del C.I.R. del movimiento {21}.
- Calcular las velocidades,
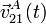 y
y 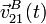 , y las aceleraciones,
, y las aceleraciones, 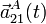 y
y 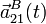 , de los dos extremos de la barra en cualquier instante de tiempo.
, de los dos extremos de la barra en cualquier instante de tiempo.
- Determinar analíticamente la posición del C.I.R. del movimiento {21}.
3 Placa en escuadra rotatoria
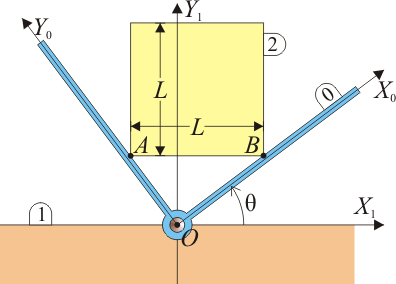
Se tiene un sistema formado por un plano horizontal (sólido “1”) en uno de cuyos puntos, O, se encuentra articulada una escuadra (sólido “0”) formada por dos barras ortogonales entre sí. Esta escuadra gira en torno a O, resultando variable el ángulo θ(t) que forma la barra OX0 con el plano horizontal “1” (ver figura). Sobre la escuadra se encuentra permanentemente apoyada por sus vértices inferiores, A y B, una placa cuadrada de lado L, cuyo lado inferior AB mantiene en todo momento su horizontalidad respecto al plano “1”.
- En función del ángulo θ, localice geométricamente de forma razonada el centro instantáneo de rotación del movimiento {20}. Exprese su vector de posición relativo al punto O tanto en la base ligada al sólido “0” como en la ligada al sólido “1”. ¿Dónde se localiza el CIR del movimiento {21}?
- En función de θ y de
 , calcule las velocidades de deslizamiento de la placa “2” respecto a la escuadra “0” en los puntos de contacto A y B.
, calcule las velocidades de deslizamiento de la placa “2” respecto a la escuadra “0” en los puntos de contacto A y B.
4 Dos rodillos con deslizamiento
Un rodillo de radio 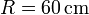 (sólido “0”) rueda sin deslizar sobre un suelo horizontal “1” de forma que su centro C avanza con una celeridad constante
(sólido “0”) rueda sin deslizar sobre un suelo horizontal “1” de forma que su centro C avanza con una celeridad constante 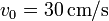 respecto al suelo. En su marcha, este rodillo empuja a un segundo rodillo de radio
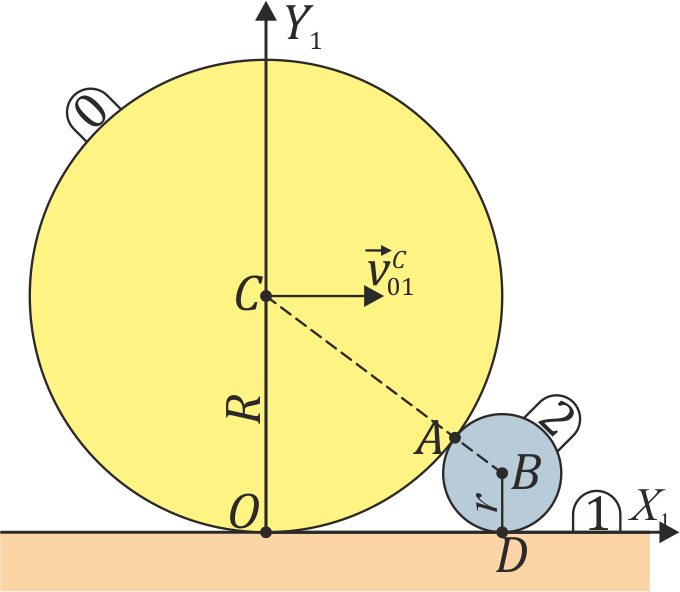
respecto al suelo. En su marcha, este rodillo empuja a un segundo rodillo de radio 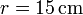 (sólido “2”), que se ve obligado a rodar sin deslizar sobre el mismo suelo, manteniéndose tangente al primer rodillo (ver figura).
(sólido “2”), que se ve obligado a rodar sin deslizar sobre el mismo suelo, manteniéndose tangente al primer rodillo (ver figura).
- Calcule las velocidades angulares
 ,
,  y
y  .
.
- Halle la velocidad relativa de deslizamiento en el punto A de contacto entre los dos sólidos
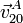 . ¿Cuál es la rapidez de este deslizamiento?
. ¿Cuál es la rapidez de este deslizamiento?
- Determine la posición del centro instantáneo de rotación I20 por los procedimientos siguientes: (i) analíticamente (con ayuda del resultado del apartado anterior); (ii) gráficamente.
5 Engranaje concéntrico
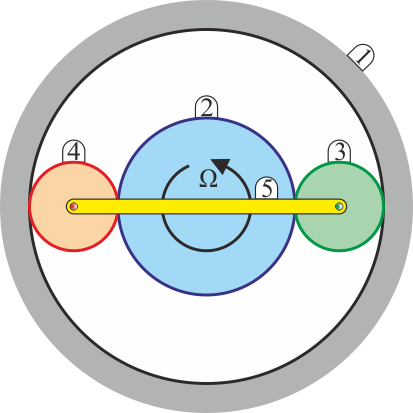
Se tiene un engranaje formado por un eje central sobre el cual va montado un disco de radio a (sólido “2”) y un anillo exterior estacionario (sólido “1”), de radio b. Entre el disco central y el anillo exterior se encuentra un sistema de dos discos iguales (“3”) y (“4”) que ruedan sin deslizar sobre ambas superficies. Los centros de estos discos se encuentran unidos por una barra articulada “5”. En un momento dado, el disco central se encuentra girando con velocidad angular Ω respecto al anillo fijo exterior y los centros de los discos 3 y 4 se encuentran sobre el eje OX1.
- Determine las velocidades angulares
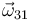 ,
, 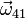 y
y 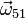 .
.
- ¿Qué tipo de movimiento efectúa el disco 3 respecto al 4? ¿Con qué velocidad?
6 Barra apoyada en placa
El esquema de la figura muestra una placa cuadrada de lado a (sólido “0”), uno de cuyos lados desliza sobre el eje horizontal fijo OX1 (sólido “1”), mientras que la placa permanece contenida siempre en el plano vertical fijo OX1Y1. Sobre el vértice A de dicha placa se apoya en todo instante una varilla delgada (sólido “2”), que gira con velocidad angular constante 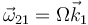 , alrededor de su extremo articulado en el punto fijo O (ver figura). Se pide:
, alrededor de su extremo articulado en el punto fijo O (ver figura). Se pide:
- Determinar gráficamente la posición de los centros instantáneos de rotación I21, I02 e I01.
- Calcular: i) La velocidad del vértice A de la placa en el movimiento de ésta respecto de los ejes fijos (movimiento {01}), expresada en función de la posición del sistema:
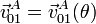 . ii) La velocidad angular
. ii) La velocidad angular  , correspondiente al movimiento relativo de la placa respecto de la varilla (movimiento {02}).
, correspondiente al movimiento relativo de la placa respecto de la varilla (movimiento {02}).
- Determinar analíticamente la posición del CIR del movimiento {02} (en función del ángulo θ).
7 Disco apoyado en placa
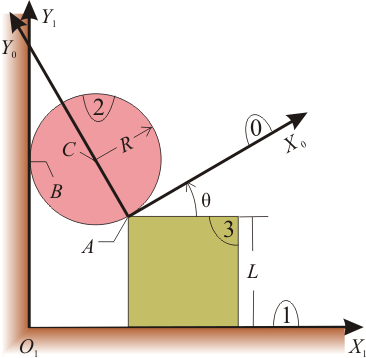
El sistema mecánico de la figura está constituido por los siguientes sólidos rígidos: El plano fijo O1X1Y1 (sólido “1”); la placa cuadrada, de lado L, que desliza sobre el eje O1X1, manteniendo su lado inferior completo en permanente contacto con él (sólido “3”); el disco, de centro en C y radio R, que, en todo instante, rueda sin deslizar sobre el eje O1Y1 en el punto de contacto B, a la vez que rueda y desliza sobre la placa cuadrada en el punto de contacto A (sólido “2”) y el sistema de ejes AX0Y0, definido de tal modo que el eje AY0 contiene permanentemente al centro C del disco, mientras que el eje AX0 es tangente a dicho disco (sólido “0”).
- Para el instante considerado en la figura, determine gráficamente la posición de los centros instantáneos de rotación I21, I20, I03, I23 e I01.
- Utilizando como parámetro el ángulo θ del dibujo (ángulo que forma el eje AX0 con respecto al lado superior de la placa cuadrada), y teniendo presentes las leyes de composición de velocidades y de velocidades angulares aplicadas a {21} = {20} + {03} + {31} halle las siguientes reducciones cinemáticas en C:
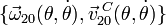 ,
,  ,
,  y
y 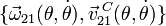 .
.
8 Disco en manivela ranurada
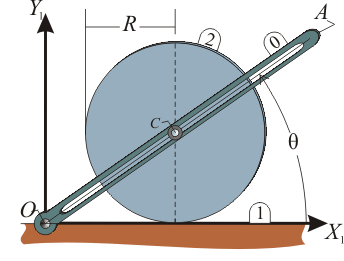
El sistema de la figura está constituido por un plano vertical fijo OX1Y1 (sólido “1”) que en todo instante contiene a otros dos sólidos en movimiento: un disco de radio R y centro C (sólido “2”), que rueda sin deslizar sobre el eje horizontal OX1; y una manivela ranurada OA (sólido “0”), que es obligada a girar con velocidad angular constante Ω alrededor de un eje permanente de rotación que pasa por el punto O y es perpendicular al plano fijo definido como sólido “1” (eje OZ1). Los movimientos de ambos sólidos se hallan vinculados entre sí porque el centro C del disco está obligado a deslizar en todo instante a lo largo de la ranura de la manivela.
Considerando el movimiento {20} como el movimiento problema, se pide:
- Haciendo uso de procedimientos gráficos, determinar la posición del C.I.R. de dicho movimiento {20}.
- Utilizando como parámetro geométrico el ángulo θ indicado en la figura, obtener la reducción cinemática del movimiento {20} en el punto C,
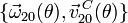 .
.
- Clasificar el movimiento {20} en el instante en que θ = π / 2 especificando si se trata de rotación, traslación, movimiento helicoidal o reposo.
9 Movimiento de dos varillas articuladas
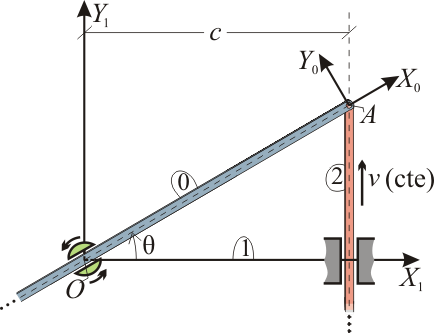
El mecanismo de la figura está constituido por dos varillas rígidas (sólidos “2” y “0”), de grosor despreciable y longitud indefinida, que se mueven en el plano fijo OX1Y1 (sólido “1”). La varilla “2” se desplaza verticalmente hacia arriba con velocidad constante v, manteniéndose siempre paralela al eje 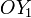 y a una distancia c de éste; mientras que la varilla “0”, articulada a la anterior en su extremo común A, desliza por el interior de un pasador giratorio ubicado en el punto O del sólido “1”. Utilizando el ángulo θ (definido en la figura) como parámetro descriptivo del movimiento, se pide:
y a una distancia c de éste; mientras que la varilla “0”, articulada a la anterior en su extremo común A, desliza por el interior de un pasador giratorio ubicado en el punto O del sólido “1”. Utilizando el ángulo θ (definido en la figura) como parámetro descriptivo del movimiento, se pide:
- Reducción cinemática de los movimientos {21}, {20} y {01} en el punto O, es decir:
 ,
, 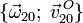 y
y  .
.
- Determinación gráfica y determinación analítica de la posición del punto I01, centro instantáneo de rotación del movimiento {01}.
- Cálculo de las aceleraciones
 y
y 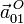 .
.
Nota: Para resolver el ejercicio, se propone el uso de la base vectorial asociada al sistema de ejes 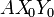 de la figura, que se mueve solidariamente con la varilla “0” y cuyo eje AX0 es colineal con ella.
de la figura, que se mueve solidariamente con la varilla “0” y cuyo eje AX0 es colineal con ella.
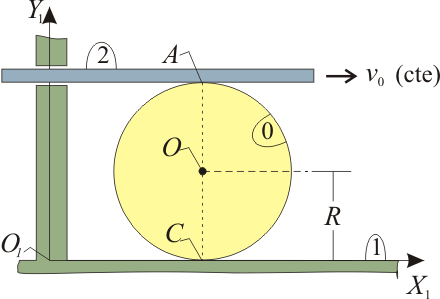
10 Barra horizontal apoyada en disco
El sistema de la figura consta de un disco (sólido “0”), de centro O y radio R, que rueda sin deslizar sobre el eje horizontal O1X1 de la escuadra fija O1X1Y1 (sólido “1”); y de una barra de longitud indefinida (sólido “2”), que se desplaza horizontalmente con velocidad constante v0, manteniéndose siempre en contacto tangente con el perímetro del disco (punto A) y sin deslizar sobre éste. Se pide:
- Reducciones cinemáticas de los movimientos {21}, {01} y {20} en el centro del disco (punto O), es decir:
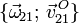 ,
, 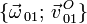 y
y 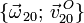 .
.
- Aceleración relativa barra-disco del punto de contacto A, es decir:
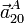 .
.
11 Barra oblicua apoyada en disco (Ex.Dic/11)
Se tiene un sistema de tres sólidos: una superficie horizontal fija (sólido "1"), una barra (sólido "0") articulada en un punto  de la superficie horizontal, y un disco
(sólido "2") de radio
de la superficie horizontal, y un disco
(sólido "2") de radio  . La barra se encuentra apoyada en el disco. El disco rueda sin deslizar sobre el suelo, moviéndose hacia la izquierda, empujando a la barra en su movimiento, de forma que el ángulo
. La barra se encuentra apoyada en el disco. El disco rueda sin deslizar sobre el suelo, moviéndose hacia la izquierda, empujando a la barra en su movimiento, de forma que el ángulo 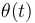 va aumentando (ver figura). Localice gráficamente las posiciones de los centros instantáneos de rotación
va aumentando (ver figura). Localice gráficamente las posiciones de los centros instantáneos de rotación  ,
, 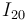 e
e 
Suponga que el disco tiene radio 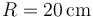 y que en un instante dado su punto de contacto con el suelo
y que en un instante dado su punto de contacto con el suelo  se encuentra a una distancia
se encuentra a una distancia 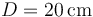 de
de 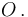 En ese momento el ángulo
En ese momento el ángulo  crece con derivada
crece con derivada 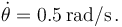 Para ese instante:
Para ese instante:
- Calcule las velocidades angulares
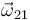 ,
, 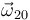 y
y 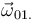
- Indique los vectores de posición, respecto al sistema de ejes "1", de los centros instantáneos de rotación.
- Halle la velocidad de deslizamiento del disco respecto a la barra en el punto de contacto
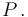
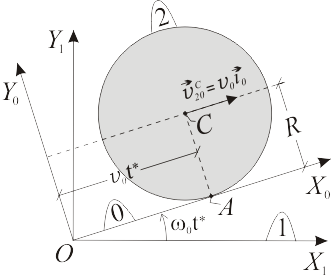
12 Disco rodando sobre escuadra giratoria (Ex.Ene/12)
Un disco de radio  (sólido "2"), contenido en el plano
(sólido "2"), contenido en el plano 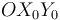 , rueda sin deslizar sobre el eje
, rueda sin deslizar sobre el eje 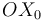 (sólido "0"), de tal modo que su centro
(sólido "0"), de tal modo que su centro  avanza con velocidad relativa constante
avanza con velocidad relativa constante 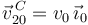 . Al mismo tiempo, la escuadra
. Al mismo tiempo, la escuadra 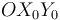 (sólido "0"), articulada en su punto
(sólido "0"), articulada en su punto  al origen de coordenadas de la escuadra fija y coplanaria
al origen de coordenadas de la escuadra fija y coplanaria  (sólido "1"), rota con velocidad angular absoluta constante
(sólido "1"), rota con velocidad angular absoluta constante 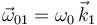 alrededor del eje fijo
alrededor del eje fijo 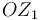 . La posición del sistema que se representa en la figura, y a la cual se refieren las siguientes preguntas, corresponde al instante
. La posición del sistema que se representa en la figura, y a la cual se refieren las siguientes preguntas, corresponde al instante 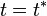 .
.
- ¿Dónde se halla el centro instantáneo de rotación
 ?
?
- Determine la aceleración instantánea
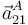 (ver
(ver  en figura).
en figura).
- ¿En qué caso particular el movimiento {21} es una traslación?
13 Disco rodando en pared (Ex.Sep/12)
El plano vertical fijo 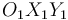 (sólido "1") de la figura contiene en todo instante a dos sólidos vinculados entre sí y en movimiento: un disco de radio
(sólido "1") de la figura contiene en todo instante a dos sólidos vinculados entre sí y en movimiento: un disco de radio  (sólido "2"), y una barra
(sólido "2"), y una barra 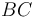 de longitud
de longitud  (sólido "0"). El disco rueda sin deslizar sobre el eje vertical
(sólido "0"). El disco rueda sin deslizar sobre el eje vertical 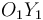 , avanzando su centro
, avanzando su centro  con velocidad constante
con velocidad constante 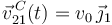 . Y, como consecuencia, también la barra se mueve, ya que su extremo
. Y, como consecuencia, también la barra se mueve, ya que su extremo  está articulado al
centro del disco, mientras que su extremo
está articulado al
centro del disco, mientras que su extremo  está articulado a un deslizador que lo obliga a recorrer el eje
está articulado a un deslizador que lo obliga a recorrer el eje 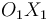 .
.
Como parámetro descriptivo de la posición del sistema, se define el ángulo  que forma la barra
que forma la barra 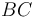 con respecto a la vertical (ver figura). Se pide:
con respecto a la vertical (ver figura). Se pide:
- Determinar gráficamente la posición de los tres centros instantáneos de rotación:
 ,
, 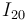 y
y 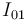 .
.
- Calcular todas las velocidades angulares en función de la posición, es decir:
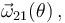
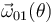 y
y 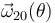 .
.
- Calcular las aceleraciones
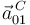 y
y 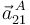 (ver
(ver  en la figura).
en la figura).