No Boletín - Area de un cuadrilátero (Ex.Nov/12)
De Laplace
1 Enunciado
¿Corresponde la siguiente fórmula al área del cuadrilátero 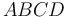 ?
?

2 Solución
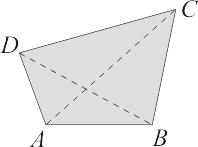
La respuesta es sí. Para comprobarlo, llamamos  al punto en el que se cortan la dos diagonales del cuadrilátero, y descomponemos cada diagonal del siguiente modo:
al punto en el que se cortan la dos diagonales del cuadrilátero, y descomponemos cada diagonal del siguiente modo:

Entonces, aplicando la propiedad distributiva del producto vectorial respecto a la suma, la fórmula puede desarrollarse así:
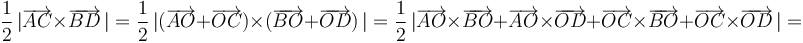
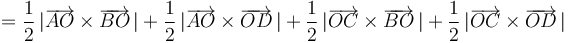
Obsérvese que los cuatro productos vectoriales a cuya suma había que calcular el módulo (penúltima expresión) tienen todos idéntica dirección y sentido (son perpendiculares al plano del cuadrilátero y de sentido saliente). Es por eso que hemos podido igualar el módulo de la suma vectorial a la suma de los módulos de los sumandos.
La última expresión a la que hemos llegado es claramente identificable (por una de las propiedades geométricas estudiadas del producto vectorial) como la suma de las áreas de los cuatro triángulos formados respectivamente por AOB, AOD, COB y COD, y por tanto queda demostrado que la expresión de la que partimos corresponde al área del cuadrilátero ABCD.