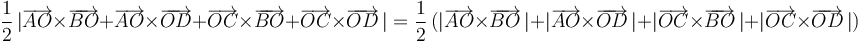No Boletín - Area de un cuadrilátero (Ex.Nov/12)
De Laplace
Revisión a fecha de 23:39 9 nov 2012; Enrique (Discusión | contribuciones)
1 Enunciado
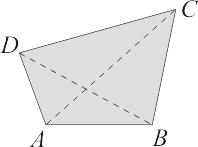
¿Es correcta la siguiente fórmula para calcular el área del cuadrilátero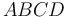 
?
2 Solución
La respuesta es sí. Para comprobarlo, llamamos 
al punto en el que se cortan la dos diagonales del cuadrilátero, y descomponemos cada diagonal del siguiente modo:
Entonces, aplicando la propiedad distributiva del producto vectorial respecto a la suma, la fórmula puede desarrollarse así:
Pero obsérvese que los cuatro productos vectoriales que aparecen sumados en la expresión a la que hemos llegado tienen todos idéntica dirección y sentido (perpendiculares al plano del cuadrilátero y de sentido saliente). Por tanto, en este caso el módulo de la suma vectorial coincide con la suma de los módulos de los sumandos:
