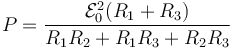Barra resistiva deslizante

De Laplace

Revisión a fecha de 18:25 10 sep 2012; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Corrientes y voltajes
3 Potencia disipada
4 Fuerza y potencia mecánica
5 Caso límite

1 Enunciado

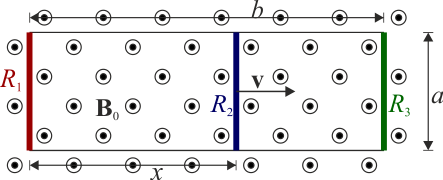
Tres barras de longitud $a$ con resistencias $R 1$ , $R 2$ y $R 3$ se encuentran conectadas por raíles perfectamente conductores (ver figura). La barra 1 y la 3 están en reposo, separadas una distancia $b$ , pero la 2 se mueve hacia la derecha con velocidad $v 0$ , siendo su distancia a la primera barra una cantidad $x (t)$ . Todo el sistema se encuentra sumergido en un campo magnético uniforme $\mathbf{B}_0$ perpendicular al circuito.

Calcule la corriente que circula por cada barra, así como el voltaje entre los extremos de cada una de ellas.
Calcule la potencia disipada en el circuito por efecto Joule.
Halle la fuerza que el campo magnético ejerce sobre la barra central. ¿Qué potencia desarrolla esta fuerza?
Considere el caso en el que la resistencia 1 es un amperímetro ( $R_1\to 0$ ) y la 3 un voltímetro ( $R_3\to\infty$ ). ¿Qué corriente marca el amperímetro y que voltaje el voltímetro?

Archivo:barra-resistiva-deslizante-00.png

2 Corrientes y voltajes

Tenemos un circuito formado por dos mallas. La fuerza electromotriz en cada una la obtenemos aplicando la ley de Faraday

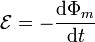
$\mathcal{E}=-\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}$

Consideramos para cada malla un sentido de recorrido antihorario, de forma que el flujo magnético sea positivo en ambas.

En la de la izquierda tenemos

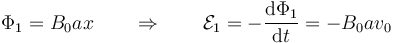
$\Phi_1 = B_0ax\qquad\Rightarrow\qquad \mathcal{E}_1 = -\frac{\mathrm{d}\Phi_1}{\mathrm{d}t}=-B_0a v_0$

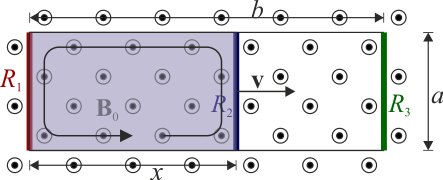
Archivo:barra-resistiva-deslizante-01.png

y en la de la derecha

$\Phi_2 = B_0a(b-x)\qquad\Rightarrow\qquad \mathcal{E}_2 = -\frac{\mathrm{d}\Phi_2}{\mathrm{d}t}=+B_0a v_0$

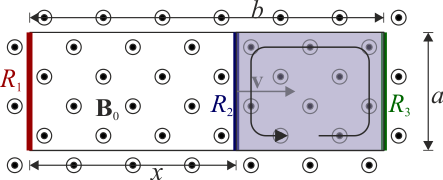
Archivo:barra-resistiva-deslizante-02.png

Vemos que resultan fuerzas electromotrices de la misma magnitud pero signo opuesto.

$\mathcal{E}_1 = -\mathcal{E}_0\qquad\qquad\mathcal{E}_2 = +\mathcal{E}_0$

lo que equivale al circuito

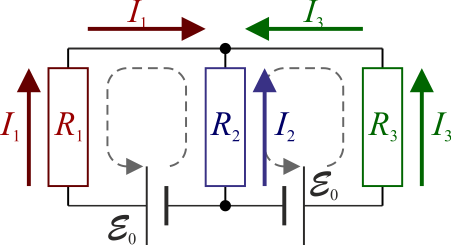
Archivo:barra-resistiva-deslizante-03.png

Para hallar la corriente por las diferentes ramas, analizamos el circuito. Suponemos sentidos de la corriente hacia arriba en cada una de las resistencias. Esto implica, por la primera ley de Kirchhoff aplicada a los nodos

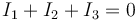
$I_1+I_2+I_3 = 0\,$

mientras que la segunda ley de Kirchhoff aplicada a la malla de la izquierda da

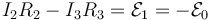
$I_2R_2-I_3R_3 = \mathcal{E}_1 = -\mathcal{E}_0$

y aplicada a la de la derecha

$I_3R_3-I_2R_2 = \mathcal{E}_2 = \mathcal{E}_0$

Tenemos entonces el sistema de ecuaciones

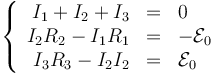
$\left\{\begin{array}{rcl} I_1+I_2+I_3 & = & 0 \\ I_2R_2-I_1R_1 & = & -\mathcal{E}_0 \\ I_3R_3-I_2I_2 & = & \mathcal{E}_0\end{array}\right.$

Sumando la segunda y la tercera queda

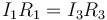
$I_1R_1 = I_3 R_3 \,$

y llevando esto a la primera

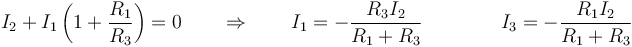
$I_2 + I_1\left(1+\frac{R_1}{R_3}\right) = 0\qquad\Rightarrow\qquad I_1 = -\frac{R_3I_2}{R_1+R_3}\qquad\qquad I_3 = -\frac{R_1I_2}{R_1+R_3}$

Sustituyendo ahora en la segunda

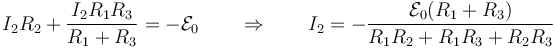
$I_2R_2 + \frac{I_2R_1R_3}{R_1+R_3} = -\mathcal{E}_0\qquad\Rightarrow\qquad I_2 = -\frac{\mathcal{E}_0(R_1+R_3)}{R_1R_2+R_1R_3+R_2R_3}$

y quedan las otras dos intensidades de corriente

$I_1 = \frac{\mathcal{E}_0R_3}{R_1R_2+R_1R_3+R_2R_3}\qquad\qquad I_3 = \frac{\mathcal{E}_0R_1}{R_1R_2+R_1R_3+R_2R_3}$

Los voltajes en cada una resultan de aplicar la ley de Ohm. Tomando el voltaje medido desde el punto inferior de la resistencia al superior queda

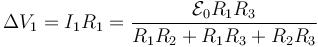
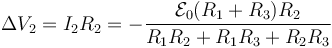
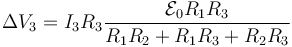
$\Delta V_1 = I_1R_1 = \frac{\mathcal{E}_0R_1R_3}{R_1R_2+R_1R_3+R_2R_3}$ $\Delta V_2=I_2R_2= -\frac{\mathcal{E}_0(R_1+R_3)R_2}{R_1R_2+R_1R_3+R_2R_3}$ $\Delta V_3 = I_3R_3\frac{\mathcal{E}_0R_1R_3}{R_1R_2+R_1R_3+R_2R_3}$

Vemos que no son los tres iguales entre sí (aunque sí lo son el 1 y el 3). Es decir, las tres resistencias no están en paralelo. Al existir un flujo magnético variable, existe una f.e.em. en cada malla que provoca que la integral sobre cada curva cerrada no sea cero (que es esencial para poder afirmar que dos elementos están en paralelo). En términos del circuito equivalente, debemos intercalar dos fuentes de tensión, que provocan que ya no estén en paralelo.

Alternativamente, puede simplificarse el análisis observando que, por ser las dos fuerzas electromotrices de la misma magnitud, pueden modelarse como una sola fuente situada en la rama central

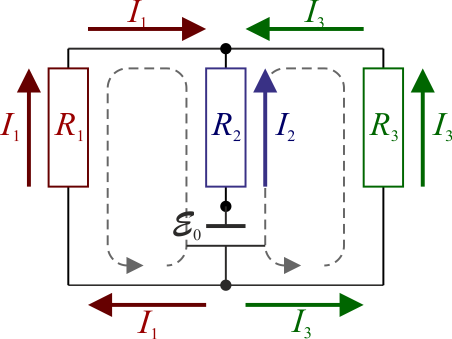
Archivo:barra-resistiva-deslizante-03b.png

De esta forma, es claro que las resistencias $R 1$ y $R 3$ están en paralelo y su asociación está en serie con $R 2$ resultando una resistencia equivalente

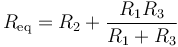
$R_\mathrm{eq} = R_2 + \frac{R_1R_3}{R_1+R_3}$

lo que nos da la corriente por la rama central

$I_2 = -\frac{\mathcal{E}_0}{R_\mathrm{eq}} = -\frac{\mathcal{E}_0(R_1+R_3)}{R_1R_2+R_1R_3+R_2R_3}$

A partir de estas corriente se hallan las otras dos considerando que se reparte por dos ramas en paralelo, de forma inversamente proporcional a la resistencia de cada una. De esta forma se llega al resultado que ya conocemos.

3 Potencia disipada

La potencia disipada la calculamos a partir del efecto Joule

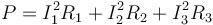
$P = I_1^2 R_1+I_2^2R_2 + I_3^2 R_3\,$

y resulta

$P = \frac{\mathcal{E}_0^2}{(R_1R_2+R_1R_3+R_2R_3)^2}(R_3^2R_1+(R_1+R_3)^2R_2 + R_1^2R_3)$

Esta expresión se puede simplificar desarrollando y factorizando el último factor

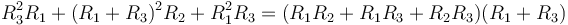
$R_3^2R_1+(R_1+R_3)^2R_2 + R_1^2R_3 = (R_1R_2+R_1R_3+R_2R_3)(R_1+R_3)$

lo que reduce la potencia a

$P = \frac{\mathcal{E}_0^2(R_1+R_3)}{R_1R_2+R_1R_3+R_2R_3}$

4 Fuerza y potencia mecánica

5 Caso límite

Barra resistiva deslizante

De Laplace

Contenido

1 Enunciado

2 Corrientes y voltajes

3 Potencia disipada

4 Fuerza y potencia mecánica

5 Caso límite

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES