Barra articulada rotatoria

De Laplace

1 Enunciado

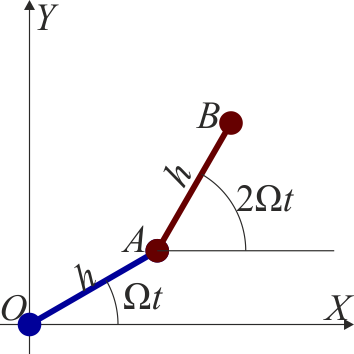
Se tiene un sistema articulado formado por dos barras de la misma masa y la misma longitud h situadas sobre una superficie horizontal. La primera barra tiene un extremo O fijo, de forma que gira alrededor de él con velocidad angular constante Ω respecto a un sistema de ejes fijos OXY. La segunda barra está articulada en el extremo A de la primera y gira respecto de los mismos ejes fijos con una velocidad angular 2Ω. En el instante t = 0 el sistema está completamente extendido a lo largo del eje OX.

1. Calcule la velocidad del punto de articulación A y del extremo libre B de la segunda barra en el instante t = 0.
2. Localice la posición del centro instantáneo de rotación I del movimiento de la segunda barra respecto a los ejes fijos para el instante t = 0.
3. Determine la posición del extremo B cuando ha pasado medio periodo, t = π / Ω, así como la velocidad de este punto en ese instante.
4. Escriba las ecuaciones horarias de la posición del punto B para todo instante.
5. Calcule la aceleración del extremo B de la barra en el instante t = 0. ¿Es nula alguna de sus componentes intrínsecas?

2 Velocidad de A y de B

2.1 Velocidad de A

2.2 Velocidad de B

3 Posición del CIR

4 B en un instante posterior

4.1 Posición

4.2 Velocidad

5 Ecuaciones horarias

6 Aceleración de B