Comparación de calores transferidos en tres procesos cuasiestáticos (F2GIA)

De Laplace

1 Enunciado

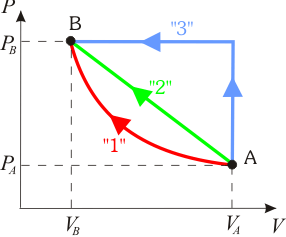
En la figura adjunta se muestran representados en un diagrama PV tres procesos termodinámicos cuasiestáticos distintos que han tenido lugar en un mismo sistema de gas ideal. Los tres procesos parten del mismo estado inicial A, y terminan en un idéntico estado final B. ¿En cuál de ellos es mayor la cantidad de calor transferida al sistema?

2 Solución

El primer principio de la Termodinámica establece la relación que guarda la variación de energía interna de un sistema termodinámico cerrado en el transcurso de un proceso, con las cantidades de calor y trabajo transferidos al sistema:

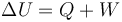
En la anterior expresión ΔU representa el incremento de energía interna experimentado al pasar de un estado inicial (A) a otro final (B), Q es el calor absorbido por el sistema en el proceso y W el trabajo realizado sobre el sistema; es decir,

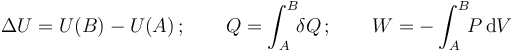
En este ejercicio, se analizan tres procesos de un sistema termodinámico, entre los mismos estados inicial, A, y final, B. Y como la energía interna es una función de estado cuyo incremento en todo proceso sólo depende de los estados inicial y final, se tendrá que en los tres procesos se experimenta la misma variación de energía interna. En consecuencia, las diferencias en las cantidades de calor absorbidas en cada proceso dependerán sólo del distinto trabajo realizado sobre el sistema en cada caso:

Por su parte, este trabajo (en valor absoluto) está representado cuantitativamente en el diagrama P − V por el área comprendida debajo de la curva P = P(V) correspondiente a dicho proceso. En los tres procesos se verifica una compresión del sistema (reducción de su volumen), por lo que los tres trabajos estarán representados por sendas cantidades positivas y las áreas bajo las curvas se corresponderán con las cantidades netas de trabajo realizados sobre el sistema:

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): W_i=-\int_{V_A("i")}^{V_B}\!\!P(V)\!\ \mathrm{d}V=\int_{V_B("i")}^{V_A}\!\!P(V)\!\ \mathrm{d}V=|W_i|>0\quad (i=1,2,3)

En los siguientes diagramas