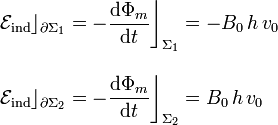Ley de Lenz en espira con barra móvil (F2GIA)
De Laplace
1 Enunciado
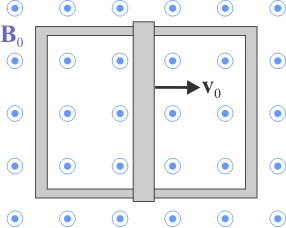
Una espira conductora rectangular fija se halla inmersa en un campo magnético uniforme y constante de magnitud B0, y dirección perpendicular al plano de la espira. Un barra conductora se desplaza con velocidad uniforme v0, manteniendo sus extremos en contacto con sendos lados paralelos de la espira. Indique los sentidos con que las corrientes eléctricas inducidas recorren cada una de mallas en que queda dividida la espira
2 Solución
La barra conductora en contacto con la espira rectangular define dos mallas o circuitos eléctricos 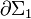 y
y 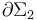 , a través de los cuales fluye el campo magnético
, a través de los cuales fluye el campo magnético  , perpendicular al plano que contiene a ambos circuitos. Obsérvese que el movimiento de la barra tiene como consecuencia que las superficies Σ1 y Σ2 delimitadas por ambos circuitos sean variables en el tiempo y, en consecuencia, también lo serán los flujos magnéticos a través de ellas. Si tomamos ambas superficies contenidas en el plano de la espira con los elementos de superficie en la misma dirección y sentido que el campo magnético, se tendrá:
, perpendicular al plano que contiene a ambos circuitos. Obsérvese que el movimiento de la barra tiene como consecuencia que las superficies Σ1 y Σ2 delimitadas por ambos circuitos sean variables en el tiempo y, en consecuencia, también lo serán los flujos magnéticos a través de ellas. Si tomamos ambas superficies contenidas en el plano de la espira con los elementos de superficie en la misma dirección y sentido que el campo magnético, se tendrá:
![\begin{array}{l}\displaystyle\Phi_m(t)\rfloor_{\Sigma_1}=\int_{\Sigma_1(t)}\!\!\mathbf{B}_0\cdot\mathrm{d}\mathbf{S}_1=B_0\!\ h\!\ x(t)\\ \\ \displaystyle\Phi_m(t)\rfloor_{\Sigma_2}=\int_{\Sigma_2(t)}\!\!\mathbf{B}_0\cdot\mathrm{d}\mathbf{S}_2=B_0\!\ h\!\ \left[l-x(t)\right]\end{array}](/wiki/images/math/5/d/f/5df4d0a06d4d08649cb1e08a2ebf97c5.png)
donde l y h son las dimensiones de la espira rectangular y x(t) la variable geométrica que mide la distancia creciente de la barra con uno de los lados de la espira. Por tanto, la derivada instantánea de este parámetro va a ser, por definición, la celeridad v0 de la barra.
En virtud de la ley de inducción electromagnética, en los circuitos 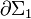 y
y 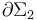 se inducirán sendas fuerzas electromotrices que en cada instante son opuestas a la variación del flujo magnético a través de los circuitos:
se inducirán sendas fuerzas electromotrices que en cada instante son opuestas a la variación del flujo magnético a través de los circuitos: