Voltaje inducido en espira alrededor de un solenoide (F2GIA)
De Laplace
1 Enunciado
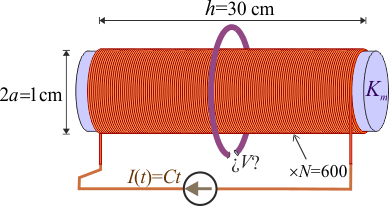
Un solenoide de longitud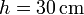 y diámetro
y diámetro 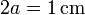 , está formado por N = 600 espiras paralelas, que se enrollan de manera compacta sobre la superficie de un cilindro de hierro cuya permeabilidad relativa es
, está formado por N = 600 espiras paralelas, que se enrollan de manera compacta sobre la superficie de un cilindro de hierro cuya permeabilidad relativa es 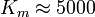 . Una anilla conductora filiforme rodea al solenoide, estando contenida en un plano perpendicular al eje del mismo y lejos de sus extremos. A la anilla le falta un pequeño trozo, de manera que constituye un circuito abierto. Si por el conductor del solenoide se hace pasar una corriente cuya intensidad crece linealmente según la ley I(t) = Ct, con
. Una anilla conductora filiforme rodea al solenoide, estando contenida en un plano perpendicular al eje del mismo y lejos de sus extremos. A la anilla le falta un pequeño trozo, de manera que constituye un circuito abierto. Si por el conductor del solenoide se hace pasar una corriente cuya intensidad crece linealmente según la ley I(t) = Ct, con 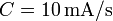 . ¿Qué tensión se medirá entre los extremos abiertos de la anilla?
. ¿Qué tensión se medirá entre los extremos abiertos de la anilla?
2 Solución
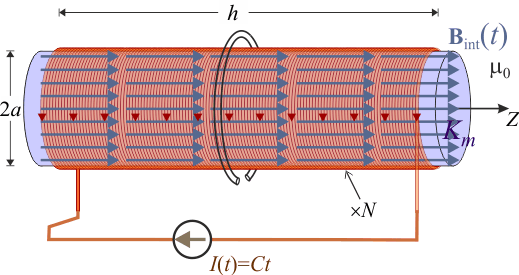
Una corriente eléctrica de intensidad I que recorre una bobina rellena de un material ferromagnético, formada por N espiras perpendiculares a su eje longitudinal y en la que es posible aplicar la aproximación de bobina larga (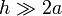 ), crea un campo magnético cuya expresión en todo el espacio es:
), crea un campo magnético cuya expresión en todo el espacio es:
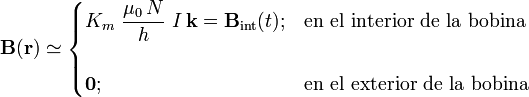
donde Km = 1 + χm es la permeabilidad magnética relativa del material ferromagnético cuando éste presenta un comportamiento lineal; como se recordará, esto ocurre si el campo magnetizante no es lo suficientemente intenso como para que el material alcance la imanación de saturación, de manera que el ferromagnético se comporta como un paramagnético de alta permeabilidad.
La anterior expresión es cierta tanto para corrientes estacionarias como variables, siempre que éstas no cambien muy rápidamente. Y suponeniendo que esta condición se verifica en el sistema analizado, se tendrá que en el interior del solenoide existirá un campo magnético prácticamente uniforme y variable en el tiempo, según la ley:

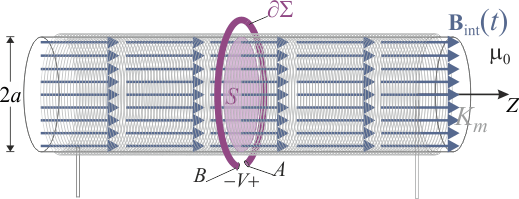
Este campo fluye a través de toda superficie abierta Σ, cuyo contorno coincida con la espira filiforme  que rodea al solenoide. Para calcular el valor de dicho flujo tomaremos la superficie delimitada por la espira y que está contenida en su mismo plano, de manera que la dirección del campo es perpendicular a dicha superficie en todos sus puntos (
que rodea al solenoide. Para calcular el valor de dicho flujo tomaremos la superficie delimitada por la espira y que está contenida en su mismo plano, de manera que la dirección del campo es perpendicular a dicha superficie en todos sus puntos (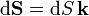 ). Por otra parte, el campo magnético sólo va a ser no nulo en el interior del solenoide, por lo que sólo habrá contribuciones al flujo magnético en la sección circular S de la bobina con ferromagnético. Y como el campo magnético en el interior es uniforme y la sección S es un círculo de radio a, se tendrá...
). Por otra parte, el campo magnético sólo va a ser no nulo en el interior del solenoide, por lo que sólo habrá contribuciones al flujo magnético en la sección circular S de la bobina con ferromagnético. Y como el campo magnético en el interior es uniforme y la sección S es un círculo de radio a, se tendrá...
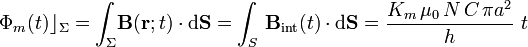
En virtud de la ley de inducción electromagnética, en la espira conductora  se inducirá una fuerza electromotriz, la cuál tendrá un valor constante mientras en el solenoide exista la corriente I(t) que genera el campo magnético de variación lineal en el tiempo.
se inducirá una fuerza electromotriz, la cuál tendrá un valor constante mientras en el solenoide exista la corriente I(t) que genera el campo magnético de variación lineal en el tiempo.
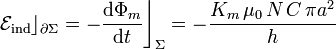
Como no hay generadores conectados  , ésta es la única f.e.m. que podría producir el movimiento de cargas eléctricas. Sin embargo, como le falta un trozo y constituye un circuito abierto, dicha fuerza electromotriz coincide con el voltaje o tensión que se puede medir entre los extremos A y B. Sustituyendo los valores de los parámetros geométricos y eléctricos que se proporcionan en el enunciado, y teniendo en cuenta que
, ésta es la única f.e.m. que podría producir el movimiento de cargas eléctricas. Sin embargo, como le falta un trozo y constituye un circuito abierto, dicha fuerza electromotriz coincide con el voltaje o tensión que se puede medir entre los extremos A y B. Sustituyendo los valores de los parámetros geométricos y eléctricos que se proporcionan en el enunciado, y teniendo en cuenta que 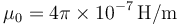 , se obtiene:
, se obtiene:

2.1 Anexo: f.e.m. inducida y tensión en los extremos de la espira
Recordemos cómo se obtenía la relación entre la fuerza electromotriz inducida en la espira abierta y la señal de tensión que se puede medir entre sus extremos. En cada punto 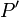 del circuito
del circuito  podemos definir una fuerza general que actúa sobre cada carga eléctrica puntual. Ésta será igual a la fuerza de Lorentz más una posible fuerza no eléctrica definida sólo en el interior de los generadores y que es responsable del movimiento de las cargas en sentido contrario al campo eléctrico. El trabajo que por unidad de carga habría de realizar esta fuerza para que las cargas puntuales completasen un circuito es, por definición, la fuerza electromotriz total en el circuito, y que será igual a la suma de la inducida más la del (los) posible(s) generadore(s) conectados:
podemos definir una fuerza general que actúa sobre cada carga eléctrica puntual. Ésta será igual a la fuerza de Lorentz más una posible fuerza no eléctrica definida sólo en el interior de los generadores y que es responsable del movimiento de las cargas en sentido contrario al campo eléctrico. El trabajo que por unidad de carga habría de realizar esta fuerza para que las cargas puntuales completasen un circuito es, por definición, la fuerza electromotriz total en el circuito, y que será igual a la suma de la inducida más la del (los) posible(s) generadore(s) conectados:
![\mathbf{F}\rfloor_{P^\prime\in\partial\Sigma}=q\left[\mathbf{E}(\mathbf{r}^\prime)+\mathbf{v}\times\mathbf{B}(\mathbf{r}^\prime)\right]+q\mathbf{E}^\prime(\mathbf{r}^\prime)\quad\Longrightarrow\mathcal{E}_\mathrm{total}\rfloor_{\partial\Sigma}=\int_{\partial\Sigma}\!\!\!\!\!\!\!\!\!\bigcirc\!\!\!\wedge\ \left[\mathbf{E}+\mathbf{v}\times\mathbf{B}+\mathbf{E}^\prime\!\ \right]\cdot\mathrm{d}\mathbf{r}^\prime=\left[\mathcal{E}_\mathrm{ind}+\mathcal{E}_\mathrm{gen}\right]_{\partial\Sigma}](/wiki/images/math/c/e/f/cefdb5b7e0703ff4339a75570bf12f3a.png)
La espira del sistema bajo estudio permanece en reposo; por tanto, su velocidad es nula en todo instante y, en consecuencia, no contribuirá a la fuerza electromotriz inducida. Además, no hay generadores conectados a la espira
Así, en cada punto del circuito se puede definir una fuerza que sobre las fuerzas realizan la relación entre la fuerza electromotriz en la espira abierta y la tensión entre los extremos d