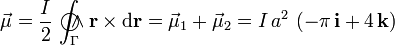Momento dipolar magnético de dos espiras planas (F2GIA)
De Laplace
1 Enunciado
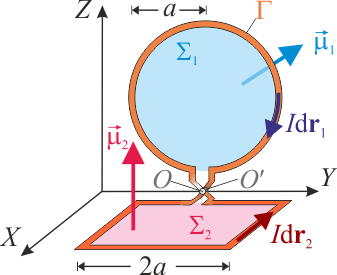
Se ha construido una antena consistente en dos pequeñas espiras planas contenidas en sendos planos ortogonales y conectadas entre sí tal como se indica en la figura. La que está situada en el plano z = 0 tiene forma cuadrada, siendo 2a la longitud de sus lados. La contenida en el plano x = 0 es una circunferencia de radio a. ¿Cuál es el momento dipolar magnético de la antena cuando una intensidad de corriente I recorre la espira cuadrada en sentido antihorario (ver figura)?
2 Solución
La antena consiste en un conductor filiforme que describe un circuito cerrado Γ. Cuando es recorrida por una corriente eléctrica con la intensidad y en el sentido indicado por el elmento de corriente 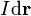 , la antena se comporta a grandes distancias como un dipolo magnético que estará caracterizado por un momento dipolar magnético,
, la antena se comporta a grandes distancias como un dipolo magnético que estará caracterizado por un momento dipolar magnético,
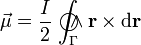
donde  es el radio-vector variable que indica la posición de los puntos del circuito respecto de un punto fijo arbitrariamente elegido. Obsérvese que, al cruzarse su trazado, existen dos puntos del conductor, O y
es el radio-vector variable que indica la posición de los puntos del circuito respecto de un punto fijo arbitrariamente elegido. Obsérvese que, al cruzarse su trazado, existen dos puntos del conductor, O y 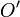 , a los que corresponden elementos de corriente distintos pero que coinciden en un mismo punto geométrico. De esta forma, la anterior integral se puede descomponer en la suma de dos integrales a lo largos de sendas curvas cerradas:
, a los que corresponden elementos de corriente distintos pero que coinciden en un mismo punto geométrico. De esta forma, la anterior integral se puede descomponer en la suma de dos integrales a lo largos de sendas curvas cerradas:
![\vec{\mu}=\frac{I}{2}\!\ \left[ \int_{O(\partial\Sigma_1)}^{O^\prime}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\bigcirc\!\!\!\!\vee\;\;\; \mathbf{r}\times\mathrm{d}\mathbf{r}+\!\ \int_{O^\prime(\partial\Sigma_2)}^O\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\bigcirc\!\!\!\!\wedge\;\;\; \mathbf{r}\times\mathrm{d}\mathbf{r}\right]](/wiki/images/math/d/4/3/d430f970f55b89ae0bf5c06e1cf12890.png)
una de forma circular, que denominaremos 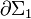 , y otra
, y otra 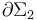 , de forma cuadrada.
, de forma cuadrada.
Pero, cada uno de los términos de la anterior expresión es, por definición el momento dipolar magnético de la espira correspondientes. Y como 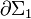 y
y  son espiras contenidas en sendos planos ortogonales, el momento dipolar de cada una de ellas será un vector de dirección perpendicular al plano de la espira y módulo igual al producto de la intensidad de corriente por el área de la superficie plana que encierra; el sentido del momento dipolar está determinado por el sentido en que la corriente recorre la espira plano, según el criterio del triedro directo:
son espiras contenidas en sendos planos ortogonales, el momento dipolar de cada una de ellas será un vector de dirección perpendicular al plano de la espira y módulo igual al producto de la intensidad de corriente por el área de la superficie plana que encierra; el sentido del momento dipolar está determinado por el sentido en que la corriente recorre la espira plano, según el criterio del triedro directo:
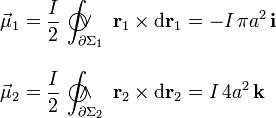
Sumando estos dos términos, obtenemos el momento dipolar magnético de la antena Γ: