Momento dipolar magnético de dos espiras planas (F2GIA)

De Laplace

1 Enunciado

Se ha construido una antena consistente en dos pequeñas espiras planas contenidas en sendos planos ortogonales y conectadas entre sí tal como se indica en la figura. La que está situada en el plano z = 0 tiene forma cuadrada, siendo 2a la longitud de sus lados. La contenida en el plano x = 0 es una circunferencia de radio a. ¿Cuál es el momento dipolar magnético de la antena cuando una intensidad de corriente I recorre la espira cuadrada en sentido antihorario (ver figura)?

2 Solución

La antena consiste en un conductor filiforme que describe un circuito cerrado Γ. Cuando es recorrida por una corriente eléctrica con la intensidad y en el sentido indicado por el elmento de corriente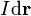 , la antena se comporta a grandes distancias como un dipolo magnético que estará caracterizado por un momento dipolar magnético,

 

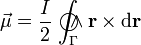
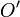donde es el radio-vector variable que indica la posición de los puntos del circuito respecto de un punto fijo arbitrariamente elegido. Obsérvese que, al cruzarse su trazado, existen dos puntos del conductor, O y , a los que corresponden elementos de corriente distintos pero que coinciden en un mismo punto geométrico. De esta forma, la anterior integral se puede descomponer en la suma de dos integrales a lo largos de sendas curvas cerradas:

una de forma circular, que denominaremos 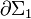, y otra 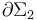, de forma cuadrada.

Pero, cada uno de los términos de la anterior expresión es, por definición el momento dipolar magnético de la espira correspondientes. Y como 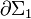y 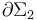son espiras contenidas en sendos planos ortogonales, el momento dipolar de cada una de ellas será un vector de dirección perpendicular al plano de la espira y módulo igual al producto de la intensidad de corriente por el área plana que encierra; el sentido del momento dipolar está determinado por el sentido en que la corriente recorre la espira plano, según el criterio del triedro directo:

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \begin{array}{l}\displaystyle\vec{\mu}_1=\frac{I}{2}\!\ \int_{\partial\Sigma_1}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\bigcirc\!\!\!\!\vee\;\;\; \mathbf{r}_1\times\mathrm{d}\mathbf{r}_1=-I\!\ \pi a^2\!\ \mathbf{i}\\ \\ \displaystyle\vec{\mu}_2=\frac{I}{2}\!\ \int_{\partial\Sigma_2}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\bigcirc\!\!\!\!\wedge\;\;\; \mathbf{r}_2\times\mathrm{d}\mathbf{r}_2=I\!\ 4 a^2\!\ \mathbf{k}

Por tanto, el cálculo del momento dipolar magnético puede descomponerse en la suma de sendos términos que, por definición, serán los momentos dipolares de cada una de las espiras descritas:

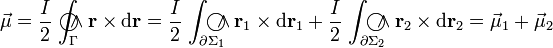
cada contenidas en sendos planos ortogonales.

Eque son distintos porque los elementos de corriente que se definen en ellos  

su trazado se cruza en el punto geométrico que coincide con los puntos físicos oemexisten dos puntos del circuito, distintos en el