Electrostática en presencia de conductores (GIE)
De Laplace
Contenido |
1 Equilibrio electrostático
La propiedad básica de los materiales conductores en electrostática es el estado de equilibrio electrostático. Este estado es aquel en que las cargas del conductor no se mueven, aunque podrían hacerlo. Si no se mueven es porque se encuentran en equilibrio y la fuerza sobre cada una de ellas es nula.
El proceso por el cual un conductor llega al equilibrio electrostático es el siguiente:
Cuando se tiene un material conductor, como puede ser una disolución salina o un metal, y se aplica un campo eléctrico externo, aparece una fuerza sobre las cargas positivas en un sentido y sobre las cargas negativas en el opuesto.
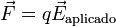
Dado que lo que caracteriza a un material conductor es que permite el movimiento de cargas por su interior, el resultado es una separación entre las cargas, las positivas a un lado y las negativas a otro.
Ahora bien, en el momento en que las cargas se separan y surgen densidades de carga opuestas, aparece un campo eléctrico adicional debido a las propias cargas del conductor, de forma que ahora la fuerza sobre cada carga del material es
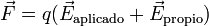
Este campo propio va en sentido opuesto al aplicado, por lo que la fuerza se reduce.
El proceso de separación de carga se detiene cuando el campo propio anula completamente al campo aplicado.
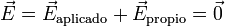
A partir de ese momento ya no hay más separación de carga y el sistema se queda en ese estado. Se ha alcanzado el equilibrio electrostático.
Si ahora se modifican las condiciones exteriores (cambiando el campo aplicado) se produce una nueva redistribución de la carga hasta que se llegue a un nuevo estado de equilibrio, en el que las cargas estarán en una posición diferente. El periodo durante el cual las cargas se están moviendo entre equilibrio y equilibrio, se denomina el periodo transitorio y suele ser muy corto en la mayoría de los materiales (microsegundos o menos).
Hay que destacar que la separación de cargas nunca llega, ni de lejos, a mover todas las cargas del material hasta llegar a agotarlas. dada la intensidad del campo eléctrico de una carga puntual, basta que una pequeñísima fracción de las cargas disponibles se separe para que lleguen a anular el campo aplicado.
En el equilibrio electrostático, las cargas están en reposo y por tanto las expresiones dadas en el tema de electrostática en el vacío siguen siendo válidas. Sin embargo, dado que las cargas de un conductor se redistribuyen continuamente a medida que cambian las condiciones externas, la densidad de carga es desconocida. Puesto que las expresiones que conocemos para el campo y el potencial presuponen que conocemos cómo se distribuyen, nos preguntamos entonces cómo podemos hallar el campo o el potencial eléctrico. Este es el denominado problema del potencial que veremos más adelante.
2 Propiedades de un conductor en equilibrio electrostático
Un conductor en equilibrio electrostático se caracteriza porque en él las cargas se encuentran en reposo, aunque tendrían la posibilidad de moverse. Esto implica una larga serie de propiedades:
- El campo eléctrico en el material conductor es nulo
- Si no fuera así, habría fuerza sobre las cargas y estas se moverían.
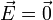
- El potencial eléctrico en todos los puntos del conductor tiene el mismo valor
- Basta tomar dos puntos A y B del conductor e integrar a lo largo de un camino que vaya íntegramente por el conductor
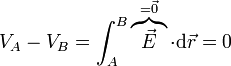
- La superficie del conductor es una superficie equipotencial
- Es un caso particular de la propiedad anterior.
- No puede hbaer líneas de campo que salgan del conductor y acaben en él
- El campo eléctrico siempre va de mayor a menor potencial y la superficie es equipotencial. Esto es cierto tanto si consideramos una línea directa, como una que pasa antes por otro sitio (por ejemplo, no puede haber una línea que vaya del conductor 1 al 2 y simultáneamente otra del 2 al 1.
- La densidad volumétrica de carga es nula
- Consideremos una superficie cerrada S cuyo volumen interior se encuentra totalmente en el material. Al aplicar la ley de Gauss
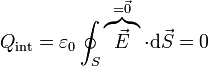
- y puesto que esto es cierto para cualquier superficie cerrada de este tipo, la conclusión es que no puede haber densidad de carga de volumen
- Esto no quiere decir que un conductor no pueda estar cargado, solo que esta carga no está repartida por el volumen.
- Toda la carga del conductor está en su superficie
- Ya que no puede haber una densidad volumétrica, toda carga que haya estará en la superficie (técnicamente, en una fina capa de varios nanómetros de espesor). Esto es así incluso en un conductor que tenga carga nula, ya que al decir que un conductor está descargado nos referimos siempre a la carga total. Puesto que un conductor está formado por billones de cargas positivas y negativas, es posible (de hecho, lo habitual) que haya una densidad de carga positiva en una parte de la superficie y negativa en otra. Esto es lo que ocurre, por ejemplo, si sobre un conductor aplicamos un campo externo.
- El campo eléctrico justo fuera del conductor es perpendicular a la superficie
- El campo eléctrico se anula dentro del conductor, pero no fuera de él. El campo exterior es una superposición del aplicado y del debido a las cargas del propio conductor (que también producen campo en el exterior). Puesto que la superficie del conductor es equipotencial, el campo eléctrico justo fuera del conductor es perpendicular a la superficie (ya que siempre es ortogonal a las equipotenciales).
- El módulo del campo exterior es proporcional a la densidad de carga superficial
- Siempre que tenemos una densidad de carga superficial (como en los ejemplos del disco, el plano o los planos cargados o la superficie esférica cargada) se produce un slato en el campo eléctrico, que depende de cuánta carga haya en la superficie. El salto es igual en todos los casos a
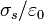. Teniendo en cuenta que en el interior del material el campo es nulo y que por la propiedad anterior el campo es perpendicular a la superficie, queda la expresión para el campo exterior
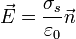
- Este campo va hacia afuera del conductor donde la densidad de carga es positiva y hacia adentro donde es negativa (ya que
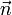es siempre la normal hacia el exterior).
- Esta última propiedad parece sugerir que no se cumple el principio de superposición, ya que si ahora a cercamos una carga puntual, ¿no sería el campo (
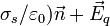es decir, la suma del que ya había más el de la carga? No, sigue siendo igual a 
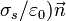. Lo que ocurre es que si acercamos una carga, las cargas del conductor se redistribuyen y σs cambia. Es decir, esta ecuación relaciona el campo en la superficie con la densidad superficial de carga, pero no nos dice cuanto vale cada una de las cantidades. La densidad de carga en un conductor también es una incógnita del problema.
3 Problema del potencial
Si las densidades de carga en los conductores son variables y desconocidas, ¿cómo puede hallarse el campo eléctrico que producen?
La forma de hacerlo es resolviendo el llamado problema del potencial, cuyo planteamiento sería aproximadamente el siguiente: tenemos un conjunto de conductores de forma arbitraria, entre los cuales se encuentra en el vacío (en el cual puede haber una densidad conocida de carga); cada uno de los conductores se encuentra a un voltaje fijado por respectivas fuentes de tensión. Se trata de hallar la distribución de potencial eléctrico entre los conductores.
De hecho, puede hallarse el potencial en todos los puntos del espacio, pero en los propios conductores es trivial (el potencial en cada uno vale el potencial fijado por cada fuente), por lo que el problema se reduce a hallar el potencial entre los conductores.
Matemáticamente este es un problema de ecuaciones diferenciales, consistente en resolver la llamada ecuación de Poisson
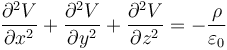
con la condición de que el potencial en la superficie de cada conductor es conocido.
En esta introducción no veremos nada de cómo se plantea y se resuelve esta ecuación (tema que da para libros y cursos enteros), pero sí un resultado esencial de la teoría del potencial:
- Teorema de existencia y unicidad
- El problema del potencial posee solución y ésta es única.
¿Por qué esta propiedad es importante? Porque primero nos garantiza que hay solución (aunque no se pueda hallar analíticamente) pero además nos dice que es única. Por tanto, cualquier método vale para hallarla, incluyendo la inspiración o la analogía con problemas similares. Si una solución propuesta cumple la ecuación diferencial y las condiciones para el potencial en la superficie de cada conductor, es la solución, porque no hay otra.
El problema del potencial es extremadamente general
