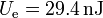Condensador plano de placas circulares
De Laplace
1 Enunciado
Se construye un condensador plano situando paralelamente dos discos conductores de 26 cm de diámetro a una distancia de 0.4 mm, entre los cuales hay aire (equivalente al vacío). Halle la capacidad del condensador y la carga y energía que almacena cuando la diferencia de potencial entre placas es de 5 V.
Suponga que rellenando el espacio entre las placas se coloca un disco dieléctrico de permitividad relativa 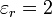 . ¿Cuánto vale en ese caso la capacidad y la carga y energía almacenadas?
. ¿Cuánto vale en ese caso la capacidad y la carga y energía almacenadas?
2 Sin dieléctrico
La capacidad de un condensador plano en vacío es

siendo el área de las placas
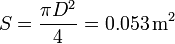
lo que da una capacidad

La carga que almacena la placa positiva del condensador cuando la d.d.p. es de 5 V vale

y la energía almacenada en el condenador

3 Con dieléctrico
El efecto de introducir un dieléctrico que llena completamente el espacio entre las placas se reduce a cambiar la permitividad del vacío por la del material

Por tanto, en este caso en que la permitividad relativa vale 2, el resultado es que la capacidad aumenta al doble
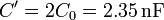
y, si se mantiene constante la tensión, aumenta al doble la carga almacenada
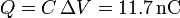
y la energía electrostática del condensador