Condensador que se rellena parcialmente de dieléctrico

De Laplace

1 Enunciado

El espacio entre dos placas metálicas circulares de 26 cm de diámetro, situadas paralelamente a una distancia 3 mm está vacío.

Entre las placas se establece una diferencia de potencial de 20 V

1. ¿Cuánto vale la energía almacenada en el sistema?
2. Suponga que, una vez cargado el condensador se desconecta la fuente y se introduce entre las placas una lámina de metacrilato (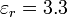) de 2 mm de espesor. ¿Cuánto cambia la energía almacenada en el sistema? ¿Cómo se explica la diferencia?
3. Suponiendo que el proceso anterior se hubiera efectuado sin desconectar la fuente, ¿cuál sería en ese caso la variación en la energía? ¿Cuánto trabajo realizaría la fuente de tensión?

2 Energía inicial

Inicialmente tenemos un condensador plano en vacío cuya capacidad es

que, cuando se encuentra a una diferencia de potencial V₀ almacena una energía

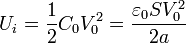
Para este sistema concreto los valores de la capacidad y la energía son

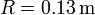    a=0.003\,\mathrm{m}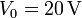                 

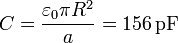
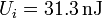
La carga almacenada en cada una de sus placas es

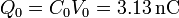
3 Energía final a carga constante

En el estado final, el sistema es uno formado por dos capas de dieléctrico, cuya capacidad equivale a la de dos condensadores puestos en serie.

            

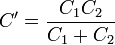
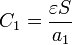
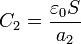
Nótese que no tenemos que especificar si la lámina de dieléctrico se encuentra adosada a una de las placas, a la otra, o no toca ninguna de las dos. Con que esté situada paralelamente a los electrodos es suficiente para obtener el resultado anterior.

En este caso concreto

                    

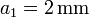
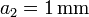
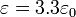
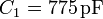
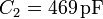
La capacidad del condensador aumenta en un 86% al introducir el dieléctrico, como consecuencia de su mayor permitividad.

En este apartado estamos suponiendo que las placas están aisladas, por lo que lo que se mantiene constante es la carga. La consecuencia del aumento en la capacidad es la reducción en la diferencia de potencial entre las placas

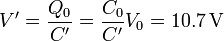
y, por tanto, de la energía almacenada, en la misma proporción

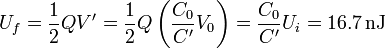
La variación de la energía almacenada en el proceso de introducir el dieléctrico es

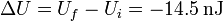
Podemos preguntarnos como se disipa energía si el sistema está aislado. La razón es que el proceso de polarización de un dieléctrico es un proceso exotérmico. Al inducir y rotar los dipolos del material, se producen fenómenos de rozamiento microscópico, que, o bien se liberan al exterior en forma de calor, o bien incrementan la temperatura del material.

4 Energía final a potencial constante

Si en el proceso de inserción del dieléctrico se realiza manteniendo conectada la fuente, entonces lo que se mantiene constante es la diferencia de potencial. El aumento de la capacidad repercute en un aumento de la carga almacenada en las placas

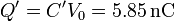
y un aumento de la energía en la misma proporción

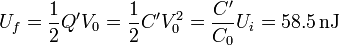
El incremento en la energía almacenada es ahora

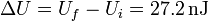
Al ser positivo este incremento parecería que el dieléctrico ahora absorbe calor o se enfría. Sin embargo, no es así. Al estar a potencial constante, existe un agente energético adicional, que es la fuente de tensión.

Para mantener la tensión fijada, la fuente añade carga a las placas, y para ello realiza un trabajo

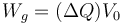
esto es, la cantidad de carga que mueve, multiplicada por la diferencia de potencial a la que la “sube”. En nuestro caso

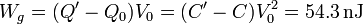
Este trabajo es exactamente el doble del aumento de la energía almacenada. Esto quiere decir que el generador realiza un trabajo extra que no se almacena como energía eléctrica, sino que se disipa en forma de calor o como un aumento de la temperatura del dieléctrico.

El valor de la energía disipada será

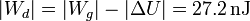
Luego el proceso es de nuevo exotérmico, como debe ser. La disipación es, de hecho, mayor que en el caso a carga constante. La razón es que en el primer caso la polarización reduce el campo eléctrico en el sistema, mientras que aquí la fuente se encarga de mantener su valor, lo que produce una mayor polarización, y una mayor disipación.