Problemas de electrostática en medios materiales (GIE)

De Laplace

1 Esfera conductora en equilibrio electrostático

Se tiene una esfera metálica maciza de radio a y no hay más conductores ni cargas en el sistema. Si la esfera almacena una carga total Q calcule:

1. el potencial y el campo eléctrico en todos los puntos del espacio.
2. el voltaje al que se encuentra
3. la densidad superficial de carga.
4. la energía electrostática que almacena.

Particularice los resultados anteriores para un radio y una carga .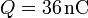

Suponga ahora que lo que se conoce inicialmente su voltaje V₀, pero no su carga. Halle en ese caso la carga que almacena, así como el resto de las cantidades obtenidas anteriormente. Particularice los resultados anteriores para un voltaje .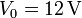

2 Carga en el interior de una corona esférica

Se tiene un conductor metálico en forma de corona esférica de radio interior 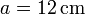y exterior 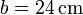. En el centro de la cavidad esférica se encuentra una carga puntual 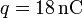. Calcule:

1. La carga en cada uno de las superficies del conductor.
2. El potencial al que se encuentra la carga y el conductor
3. El campo eléctrico en el exterior de la esfera y en la cavidad.
4. La energía electrostática almacenada.

para los siguientes cuatro casos:

• La corona esférica está conectada a tierra.
• La corona está aislada y descargada.
• La corona está conecta a una fuente de tensión que fija un voltaje .
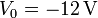• La corona está aislada y almacena una carga .

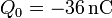3 Condensador plano de placas circulares

Se construye un condensador plano situando paralelamente dos discos conductores de 26 cm de diámetro a una distancia de 0.4 mm, entre los cuales hay aire (equivalente al vacío). Halle la capacidad del condensador y la carga y energía que almacena cuando la diferencia de potencial entre placas es de 5 V.

Suponga que rellenando el espacio entre las placas se coloca un disco dieléctrico de permitividad relativa 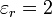$. ¿Cuánto vale en ese caso la capacidad y la carga y energía almacenadas?

4 Tres placas conductoras paralelas

Se colocan paralelamente tres placas metálicas cuadradas de 20 cm de lado y espesor despreciable, estando la primera separada de la segunda una distancia de 0.2\,mm y ésta de la tercera 0.8\,mm. Halle:

1. La carga almacenada en cada placa.
2. El potencial al que se encuentra cada una.
3. El campo eléctrico entre las placas.
4. La energía almacenada en el sistema.

para los siguientes casos:

• La placa central está aislada y descargada, la primera a 24 V y la tercera a tierra.
• La placa central está a 24 V y las otras dos a tierra.
• La primera está a -24\,V, la central a +24\,V y la tercera a tierra.

5 Cuatro placas conductoras paralelas

Se colocan paralelamente cuatro placas metálicas cuadradas de 20\,cm de lado y espesor despreciable, estando la primera separada de la segunda una distancia de 0.2\,mm, ésta de la tercera 0.4\,mm, y esta de la cuarta 0.6\,mm. Las dos placas centrales están aisladas y descargadas. Se coloca la primera placa a 100\,V y la última a tierra. Halle el voltaje y la carga de cada placa, así como la energía almacenada.

Sin desconectar la fuente de tensión se conectan por un hilo metálico la segunda con la tercera placa. Halle las nuevas cargas, voltajes y energía almacenada.

¿Cómo cambian los resultados si antes de conectar las placas centrales se desconecta la fuente de tensión?

6 Condensador que se rellena parcialmente de dieléctrico

Entre dos placas conductoras cuadradas de lado 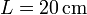y separadas una distancia 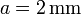entre las cuales hay aire se aplica una diferencia de potencial 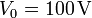. Halle la energía almacenadas en el sistema.

Suponga que, sin descargarlas, se desconectan las placas de las fuentes. En ese momento se introduce entre las placas una lámina de metacrilato (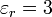) de 1 mm de espesor y misma sección que las placas, situándose paralelamente a éstas. Calcule la nueva diferencia de potencial entre las placas y la energía almacenada.

Suponga ahora que partiendo del estado inicial se introduce la lámina dieléctrica sin desconectar las placas de la fuente. ¿Cuál es en ese caso la variación en la energía almacenada? ¿Qué trabajo ha realizado la fuente de tensión?