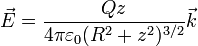Campo eléctrico de un anillo y un disco

De Laplace

1 Enunciado

Calcule, por integración directa, el campo eléctrico en los puntos del eje de un anillo de radio R que almacena una carga Q distribuida uniformemente.

A partir del resultado anterior calcule el campo en los puntos del eje de un disco circular de radio R, en el cual existe una carga Q distribuida uniformemente.

2 Anillo

Calculamos el campo eléctrico empleando el principio de superposición. Consideramos el anillo formado por pequeños elementos de carga, cada una de los cuales produce una contribución diferencial al campo

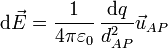
siendo d_AP la distancia entre el punto A donde se encuentra el elemento de carga y el punto P donde queremos hallar el campo. 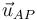es el vector unitario en la dirección de la recta que pasa por A y P y lleva el sentido de A a P.

En el caso del anillo con una carga uniformemente distribuida, dividimos el anillo en segmentos de longitud dl, cada uno de los cuales tiene una carga

La distancia entre cada punto del anillo y un punto del eje es la misma para todos ellos. Por el teorema de Pitágoras

siendo z la altura del punto de observación sobre el anillo. Esta coordenada puede ser positiva o negativa.

El vector , en cambio, depende del punto del anillo que crea el campo diferencial, de forma que tenemos

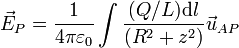
Cuando sumamos las contribuciones de puntos opuestos del anillo, las componentes paralelas al plano del anillo se anulan mutuamente, como en el caso de dos cargas iguales. Las componentes en la dirección del eje se suman. Por ello, la resultante, el campo en el punto P, posee la dirección del eje Z. La contribución de cada elemento de carga en esta dirección es

y el campo total es

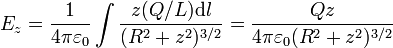
La integral es inmediata, ya que el integrando está constituido por cantidades que no dependen del punto del anillo y son por tanto constantes respecto a la integración. El cálculo se reduce entonces

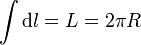
que se cancela con el que aparece en el denominador.

En forma vectorial este campo se expresa

3 Disco