Campo y potencial de una esfera con hueco

De Laplace

Revisión a fecha de 09:43 25 abr 2012; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Campo en el hueco
3 Campo exterior
4 Diferencia de potencial

1 Enunciado

Se tiene una carga 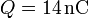$Q=14\,\mathrm{nC}$ distribuida uniformemente en una esfera maciza de radio 10.0 cm en la que se ha horadado una cavidad esférica de radio 5.0 cm cuyo centro está a 5.0 cm de la esfera grande.

Demuestre que el campo en el interior de la cavidad es uniforme y halle su valor.
Calcule el valor del campo en el exterior de la esfera en un punto situado sobre la recta que une los dos centros, a una distancia de 25 cm del centro de la esfera grande.
Calcule la diferencia de potencial entre los dos puntos diametralmente opuestos de la superficie exterior situados en la recta que pasa por los dos centros.

2 Campo en el hueco

Aunque está compuesto por esferas, este problema no tiene simetría esférica, es decir, el campo eléctrico a un lado de la esfera no es el mismo que al lado opuesto (no es lo mismo estar dentro del hueco que fuera de él). Por ello, no se puede resolver aplicando directamente la ley de Gauss.

Para hallar la solución, lo más simple es aplicar el principio de superposición. La distribución de carga de la esfera hueca puede verse como una superposición de dos distribuciones:

Una esfera maciza de radio $a$ , con una densidad de carga $+ ρ 0$
Una esfera maciza de radio $a / 2$ descentrada respecto a la anterior y de densidad de carga $- ρ 0$

En los puntos en que coinciden, que son los del hueco, la carga en cada elemento de volumen es

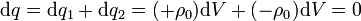
$\mathrm{d}q = \mathrm{d}q_1+\mathrm{d}q_2 = (+\rho_0)\mathrm{d}V+(-\rho_0)\mathrm{d}V = 0\,$

Nótese que la superposición debe hacerse sobre densidades de carga, no sobre la carga total (ya que lo que se suma es la carga en cada punto).

Puesto que la distribución es uniforme, la densidad de carga la obtenemos dividiendo la carga total por el volumen donde se encuentra (que es el de la esfera menos el hueco esférico)

$\rho_0 = \frac{Q}{4\pi a^3/3 - 4\pi(a/2)^3/3}= \frac{6Q}{7\pi a^3}$

El campo en el interior de una esfera maciza cargada uniformemente se puede hallar por aplicación de la ley de Gauss y tiene la expresión general

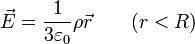
$\vec{E}=\frac{1}{3\varepsilon_0}\rho\vec{r}\qquad (r < R)$

Donde $\vec{r}$ es el vector de posición respecto al centro de la esfera. En nuestro caso, debemos considerar un centro diferente para la esfera completa y para el hueco, el cual está centrado en

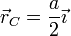
$\vec{r}_C = \frac{a}{2}\vec{\imath}$

considerando ejes centrados en la esfera grande y con el eje OX en la línea que une los centros.

Aplicando el principio de superposición nos queda el campo total en un punto P del hueco

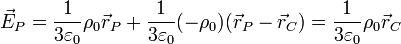
$\vec{E}_P = \frac{1}{3\varepsilon_0}\rho_0\vec{r}_P+\frac{1}{3\varepsilon_0}(-\rho_0)(\vec{r}_P-\vec{r}_C) = \frac{1}{3\varepsilon_0}\rho_0\vec{r}_C$

Vemos que el resultado es independiente de la posición de P, ya que solo aparece la posición del centro del hueco. Por tanto, en todos los puntos de la cavidad el campo tiene el mismo valor. Las líneas de campo en esta región serán rectas paralelas al eje que pasa por los centros.

En función de la carga total, este campo vale

$\vec{E}_P= \frac{1}{3\varepsilon_0}\left(\frac{6Q}{7\pi a^3}\right)\left(\frac{a}{2}\vec{\imath}\right)=\frac{Q}{7\pi\varepsilon_0 a^3}\vec{\imath}$

siendo su valor numérico

$\vec{E}_P = \frac{14\times 10^{-9}}{7\pi\times 8.85\times 10^{-12}\times 0.1^3}\vec{\imath}\frac{\mathrm{V}}{\mathrm{m}}=72\,\vec{\imath}\frac{\mathrm{kV}}{\mathrm{m}}$

3 Campo exterior

4 Diferencia de potencial

Campo y potencial de una esfera con hueco

De Laplace

Contenido

1 Enunciado

2 Campo en el hueco

3 Campo exterior

4 Diferencia de potencial

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES