Proceso de carga de una esfera conductora (F2GIA)

De Laplace

1 Enunciado

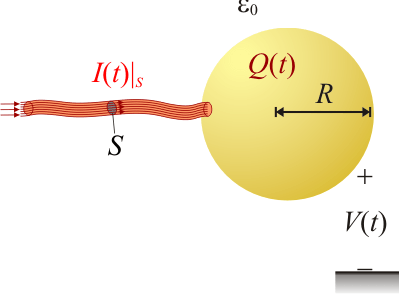
A una esfera metálica de radio R, inicialmente descargada, llega una corriente eléctrica a través de un delgado hilo conductor. La intensidad de la corriente decae exponencialmente en el tiempo según la ley I(t) = I₀e ^{− t / τ}, donde I₀ es la intensidad de corriente inicial y τ es un valor constante con dimensiones de tiempo (constante de relajación). ¿Cómo será el valor del potencial electrostático en la esfera al cabo de un tiempo suficientemente grande ()?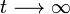

2 Solución

La intensidad de corriente que circula por el cable conductor describe la cantidad de carga que por unidad de tiempo cruza cualquiera de sus secciones S. Dicha carga llega a la esfera conductora, donde se irá acumulando. Aplicando el principio de conservación de la carga, se tendrá que la variación instantánea de la cantidad de carga Q(t) en la esfera será igual a la intensidad de corriente que circula por el cable:

 

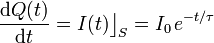
Por tanto, para obtener la cantidad total de carga Q_f que almacenará la esfera al cabo de un intervalo de tiempo muy grande, no hay más que integrar la anterior ecuación diferencial con la condición de que en el instante inicial (cuando empieza a circular la corriente) la esfera está descargada:

Puede comprobarse que el proceso de carga de la esfera sigue una ley exponencial con la cantidad Q_f como valor límite, de manera que en un instante arbitrario t, la cantidad de carga almancenada será,

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): Q(t)=I\0\!\ \tau \left(1-e^{-t/\tau}\right)