Dos esferas metálicas conectadas a potencial fijo (F2GIA)

De Laplace

Revisión a fecha de 18:34 21 abr 2012; Gabriel (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

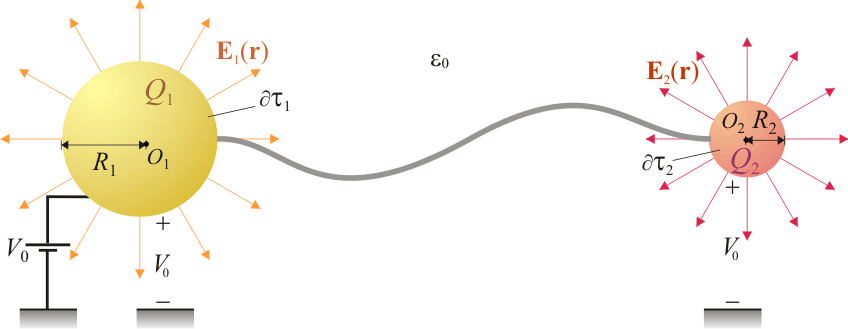
Dos esferas metálicas conductoras de distintos radios, $R 1$ y $R 2$ , se encuentran muy alejadas entre sí, aunque conectadas mediante un hilo conductor perfecto de gran longitud. La esfera mayor (de radio $R 1$ ) está conectada a un generador ideal de fuerza electromotriz $V 0$ . Asumiendo que la distancia de separación entre las esferas es suficiente como para considerar que no hay influencia entre ellas, analice los valores del potencial, carga eléctrica, densidad superficial de carga e intensidad del campo eléctrico en las superficies de ambos conductores.

2 Solución

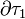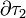Las dos esferas metálicas están conectadas mediante un hilo que se considera conductor perfecto. Por tanto, cuando tras conectar la esfera mayor al generador ideal, el sistema alcanza el equilibrio electrostático, el valor del potencial en ambas esferas será $V 0$ . En particular, la superficies esféricas $\partial\tau_1$ y $\partial\tau_2$ serán equipotenciales:

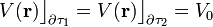
$V(\mathbf{r})\big\rfloor_{\partial\tau_1}=V(\mathbf{r})\big\rfloor_{\partial\tau_2}=V_0$

En ellas se almacenerán sendas cantidades de carga eléctrica, $Q 1$ y $Q 2$ . Se considera que las esferas están lo suficientemente alejadas como para que no haya una influencia apreciable entre ellas. Por tanto, la relación entre la cantidad de carga y el valor del potencial en cada superficie estará determinado por el correspondiente valor de su capacidad eléctrica.

$Q_1=C_1\!\ V_0\,\mathrm{;}\,\qquad Q_2=C_2\!\ V_0$

Si además de considerar las esferas muy alejadas, despreciamos el posible efecto del cable conductor, podemos asumir que la carga eléctrica se distribuye homogéneamente en cada una de las superficies, de manera que los valores $C 1$ y $C 2$ serán los correspondientes a las capacidades eléctricas de superficies eléctricas de radios $R 1$ y $R 2$ . 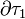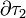Recordemos cómo se obtenían tales valores: las distribuciones uniformes de carga eléctrica en las superficies $\partial\tau_1$ y $\partial\tau_2$ crearán sendos campos potenciales electrostáticos en los entorno de cada esfera:

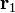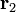$V_1(\mathbf{r})=k_e\ \frac{Q_1}{|\mathbf{r}-\mathbf{r}_1|}\,\mathrm{;}\,\qquad V_2(\mathbf{r})=k_e\ \frac{Q_2}{|\mathbf{r}-\mathbf{r}_2|}$

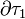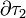donde $\mathbf{r}_1$ y $\mathbf{r}_2$ son los radiovectores que indican la posición de los centros de las esferas, $O 1$ y $O 2$ , respecto del punto elegido como origen del sistema de referencia. Los puntos de las superficies esféricas $\partial\tau_1$ y $\partial\tau_2$ se hallan a distancias $R 1$ y $R 2$ , de sus respectivos centros; por tanto,

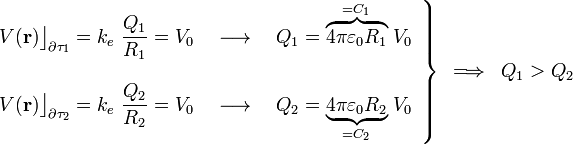
$\left.\begin{array}{l}\displaystyle V(\mathbf{r})\big\rfloor_{\partial\tau_1}=k_e\ \frac{Q_1}{R_1}=V_0\quad\longrightarrow\quad Q_1=\overbrace{4\pi\varepsilon_0R_1}^{=C_1}\!\ V_0\\ \\ \displaystyle V(\mathbf{r})\big\rfloor_{\partial\tau_2}=k_e\ \frac{Q_2}{R_2}=V_0\quad\longrightarrow\quad Q_2=\underbrace{4\pi\varepsilon_0R_2}_{=C_2}\!\ V_0\end{array}\right\}\;\,\Longrightarrow\;\;Q_1>Q_2$

Y puesto que hemos asumido que las cargas se distribuyen uniformemente, las densidades superficiales en cada una de las esferas conductoras serán,

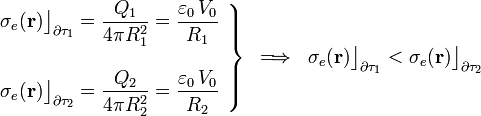
$\left.\begin{array}{l}\displaystyle \sigma_e(\mathbf{r})\big\rfloor_{\partial\tau_1}=\frac{Q_1}{4\pi R_1^2}=\frac{\varepsilon_0\!\ V_0}{R_1}\\ \\ \displaystyle \sigma_e(\mathbf{r})\big\rfloor_{\partial\tau_2}=\frac{Q_2}{4\pi R_2^2}=\frac{\varepsilon_0\!\ V_0}{R_2}\end{array}\right\}\;\,\Longrightarrow\;\;\sigma_e(\mathbf{r})\big\rfloor_{\partial\tau_1}<\sigma_e(\mathbf{r})\big\rfloor_{\partial\tau_2}$

Las cargas $Q 1$ y $Q 2$ crean sendos campo eléctricos,

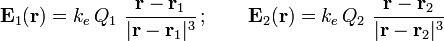
$\mathbf{E}_1(\mathbf{r})=k_e\!\ Q_1\ \frac{\mathbf{r}-\mathbf{r}_1}{|\mathbf{r}-\mathbf{r}_1|^3}\,\mathrm{;}\,\qquad \mathbf{E}_2(\mathbf{r})=k_e\!\ Q_2\ \frac{\mathbf{r}-\mathbf{r}_2}{|\mathbf{r}-\mathbf{r}_2|^3}$

en las proximidades de los conductores. La intensidad de estos campos en las superficies conductoras son:

$\left.\begin{array}{l}\displaystyle |\mathbf{E}_1(\mathbf{r})|_{\partial\tau_1}=\frac{Q_1}{4\pi \varepsilon_0 R_1^2}=\frac{V_0}{R_1}=\frac{\sigma_e(\mathbf{r})}{\varepsilon_0}\bigg\rfloor_{\partial\tau_1}\\ \\ \displaystyle |\mathbf{E}_2(\mathbf{r})|_{\partial\tau_2}=\frac{Q_2}{4\pi \varepsilon_0 R_2^2}=\frac{V_0}{R_2}=\frac{\sigma_e(\mathbf{r})}{\varepsilon_0}\bigg\rfloor_{\partial\tau_2}\end{array}\right\}\;\,\Longrightarrow\;\;|\mathbf{E}_1(\mathbf{r})|_{\partial\tau_1}<|\mathbf{E}_2(\mathbf{r})|_{\partial\tau_2}$

Dos esferas metálicas conectadas a potencial fijo (F2GIA)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES