Cálculos de carga total, campo y potencial
De Laplace
Contenido |
1 Enunciado
Calcule la carga total de las siguientes distribuciones de carga:
- N cargas de valor q situadas en los vértices de un polígono regular de N lados situado en el plano XY, con centro el origen y cuyo primer vértice se encuentra en
.
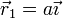- Un anillo circular de radio R con una densidad lineal de carga uniforme λ0.
- Un anillo circular de radio R con centro el origen y situado en el plano XY, con una densidad lineal de carga
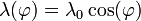, siendo 
el ángulo del vector de posición con el eje OX.
- Una superficie esférica de radio a con una densidad de carga uniforme σ0, rodeada por una superficie esférica concéntrica de radio b con densidad de carga − σ0.
- Una esfera maciza de radio R con densidad de carga uniforme ρ0.
- Una esfera maciza de radio R con una densidad de carga dependiente de la distancia al centro como
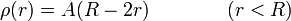
Calcule el campo y el potencial eléctrico en el origen de coordenadas para todos los sistemas del problema
2 Cargas en un polígono
2.1 Carga total
En un sistema de cargas puntuales, la carga total es la suma de todas ellas. Puesto que en este caso son todas iguales, el resultado es simplemente
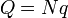
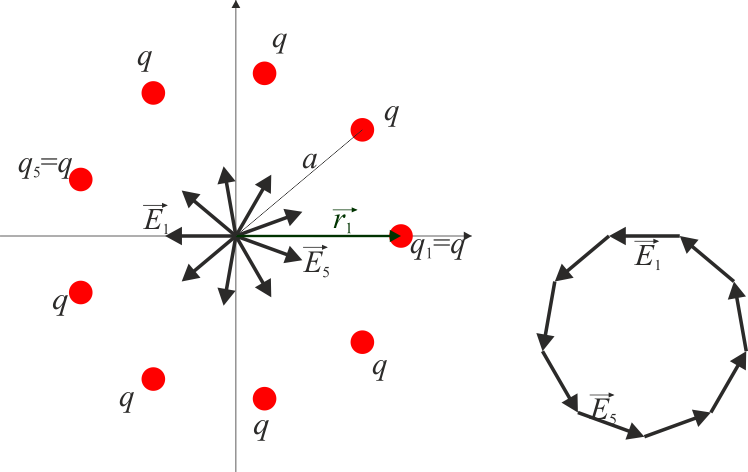
2.2 Campo eléctrico en el origen
El campo eléctrico creado por una distribución de cargas es la suma vectorial de los campos individuales
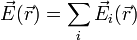
En un polígono regular todas las cargas están a la misma distancia del centro, por lo que el módulo del campo que cada una produce en el centro es el mismo para todas ellas
Esto no quiere decir que todas las cargas produzcan el mismo campo en el origen, ya que la dirección y el sentido de cada uno es diferente.
La dirección del campo de cada una de las cargas es en la dirección radial desde la carga hacia el punto O y su sentido será alejándose de la carga si esta es positiva y hacia ella si es negativa.
La suma de todos los campos que tienen el mismo módulo y van en la dirección radial mencionada, es nula.
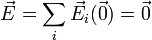
Si el número de cargas es par, el hecho es evidente. El campo de cada carga se cancela con el de la carga opuesta y el resultado es un campo nulo.
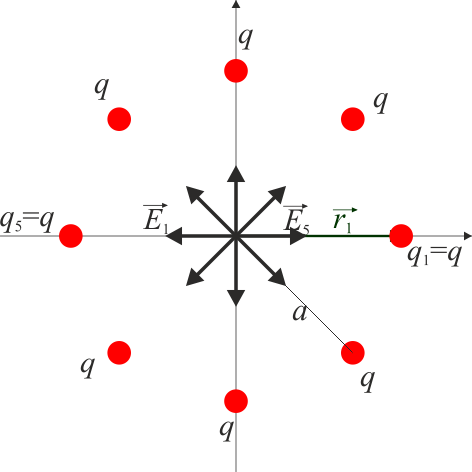
El resultado también es cierto si el número de cargas en impar. En ese caso, podemos hallar el campo resultante en el origen sumando vectorialmente los campos individuales a base de situar uno a continuación del siguiente. El resultado es otro polígono regular en el que el extremo del último vector coincide con el origen del primero, siendo la resultante nula.
