Calentamiento ineficiente de una casa

De Laplace

Revisión a fecha de 18:31 18 mar 2012; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 COP relativo
3 Producción de entropía
4 Consumo extra

1 Enunciado

En una casa de la que escapa un flujo de calor de 80000 kJ/h cuando la temperatura exterior es de 15°C y la interior se mantiene constante a 22°C se emplean estufas de resistencia eléctrica. Determine el coeficiente de desempeño relativo al máximo posible, la producción de entropía por hora y el consumo extra respecto a una bomba de calor reversible.

2 COP relativo

En una estufa de resistencia eléctrica, todo el calor que se produce proviene exclusivamente del trabajo eléctrico realizado, por lo que su coeficiente de desempeño es simplemente

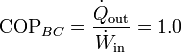
$\mathrm{COP}_{BC}= \frac{\dot{Q}_\mathrm{out}}{\dot{W}_\mathrm{in}} = 1.0$

El COP máximo que podría alcanzarse con una bomba de calor lo da el de una reversible

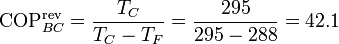
$\mathrm{COP}^\mathrm{rev}_{BC}= \frac{T_C}{T_C-T_F}=\frac{295}{295-288}=42.1$

por lo que el valor relativo al máximo posible es

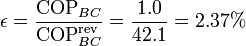
$\epsilon = \frac{\mathrm{COP}_{BC}}{\mathrm{COP}^\mathrm{rev}_{BC}}=\frac{1.0}{42.1} = 2.37\%$

Vemos que la estufa de resistencia es absolutamente ineficiente.

3 Producción de entropía

La cantidad de entropía generada por la estufa vale teniendo en cuenta que simplemente entrega calor a un foco a 22°C

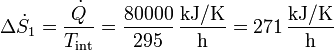
$\Delta \dot{S}_1 =\frac{\dot{Q}}{T_\mathrm{int}}=\frac{80000}{295}\,\frac{\mathrm{kJ}/\mathrm{K}}{\mathrm{h}} = 271\,\frac{\mathrm{kJ}/\mathrm{K}}{\mathrm{h}}$

Esta cantidad se ve incrementada por el hecho de que el calor escapa al exterior, que está a 15°C, siendo la producción de entropía correspondiente

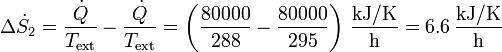
$\Delta \dot{S}_2 =\frac{\dot{Q}}{T_\mathrm{ext}}-\frac{\dot{Q}}{T_\mathrm{ext}}=\left(\frac{80000}{288}-\frac{80000}{295}\right)\,\frac{\mathrm{kJ}/\mathrm{K}}{\mathrm{h}} = 6.6\,\frac{\mathrm{kJ}/\mathrm{K}}{\mathrm{h}}$

Siendo el total de producción de entropía la misma que si el calor de la estufa se arrojara directamente al exterior:

$\Delta \dot{S} = \Delta \dot{S}_1 +\Delta \dot{S}_2 = \frac{80000}{288}\,\frac{\mathrm{kJ}/\mathrm{K}}{\mathrm{h}} = 278\,\frac{\mathrm{kJ}/\mathrm{K}}{\mathrm{h}}$

4 Consumo extra

Calentamiento ineficiente de una casa

De Laplace

Contenido

1 Enunciado

2 COP relativo

3 Producción de entropía

4 Consumo extra

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES