Sucesión de tres procesos cuasiestáticos
De Laplace
Revisión a fecha de 17:46 1 mar 2012; Antonio (Discusión | contribuciones)
Contenido |
1 Enunciado
Un cilindro de 20 cm de diámetro contiene aire y está cerrado por un émbolo. Inicialmente el aire tiene una temperatura de 27 °C y una presión de 100 kPa, que también es la presión exterior, estando el émbolo a 10 cm del fondo. Entonces se realiza el siguiente proceso cuasiestático
- I: Se atornilla el émbolo y se calienta el aire hasta 327 °C, sumergiéndolo en un baño a esta temperatura.
- II: Se libera el émbolo lentamente, dejando que se expanda el aire hasta que su presión vuelve a ser la inicial. En este proceso el aire se mantiene a la temperatura de 327 °C.
- III: Con el émbolo libre, se enfría gradualmente hasta que la temperatura vuelve a ser la inicial.
Para este proceso:
- Halle la presión, volumen y temperatura al final de cada fase del proceso.
- Calcule el trabajo en cada fase, así como el trabajo neto total.
- Calcule la variación en la energía interna y el calor en cada paso y su variación neta.
2 Presión, volumen y temperatura
2.1 Estado inicial
Inicialmente tenemos que la presión y la temperatura valen

mientras que el volumen es el de un cilindro

2.2 Tras el paso I
El primer paso ocurre a volumen constante, por estar el pistón atornillado, con lo que el voluemn final es el mismo que el inicial

La temperatura ha aumentado en 300°C
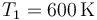
y la presión aumenta en la misma proporción que la temperatura






