Trabajo en un gas con resorte

De Laplace

Revisión a fecha de 16:09 28 feb 2012; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Se tiene un cilindro de sección $S$ en el interior del cual hay un pistón que puede deslizarse sin rozamiento. El pistón cierra una cámara en la que hay un gas ideal. La cara exterior del pistón está unida al extremo del tubo mediante un resorte de constante $k$ y longitud natural $l 0$ . Esta parte del tubo está abierta a la atmósfera. Para un cierto valor de la temperatura, $T 0$ , la presión es la atmosférica, el pistón se encuentra a una distancia $h 0$ del fondo y el resorte no ejerce fuerza alguna. Cuando el gas se calienta, se expande y el resorte se comprime.

Halle el trabajo realizado sobre el gas cuando su temperatura pasa de $T 0$ a $T 1$ .
Calcule la variación de la energía interna del gas y el calor transferido al gas en el proceso.
Calcule el trabajo, la variación en la energía total y el calor, si consideramos que el sistema esta formado por el gas y el muelle.

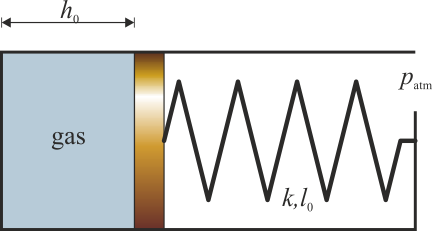
1.1 Trabajo sobre el gas

Cuando el émbolo se encuentra a una distancia $x$ de su posición inicial, el volumen ocupado por el gas es

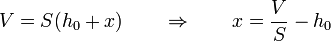
$V = S(h_0+x)\qquad\Rightarrow\qquad x = \frac{V}{S}-h_0$

el muelle se ha comprimido en esta distancia y la presión externa sobre el gas es

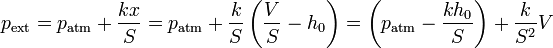
$p_\mathrm{ext}=p_\mathrm{atm}+ \frac{kx}{S} = p_\mathrm{atm} + \frac{k}{S}\left(\frac{V}{S}-h_0\right)=\left(p_\mathrm{atm}-\frac{kh_0}{S}\right)+\frac{k}{S^2}V$

por lo que el trabajo en una expansión del gas vale

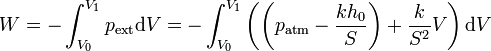
$W = -\int_{V_0}^{V_1}p_\mathrm{ext}\mathrm{d}V = -\int_{V_0}^{V_1}\left(\left(p_\mathrm{atm}-\frac{kh_0}{S}\right)+\frac{k}{S^2}V\right)\mathrm{d}V$

Integrando esta función en la que la única variable es el volumen

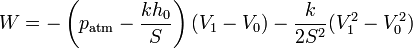
$W = -\left(p_\mathrm{atm}-\frac{kh_0}{S}\right)(V_1-V_0)-\frac{k}{2S^2}(V_1^2-V_0^2)$

Para poner este resultado en función de la temperatura observamos que en el estado inicial la presión es la atmosférica y la temperatura es $T 0$ . Cuando se pone a temperatura $T 1$

$p_1 = p_\mathrm{atm}+\frac{kx}{S}\qquad\qquad V_1 = S(h_0+x)\qquad\qquad T_1 = \frac{p_1V_1}{p_0V_0}T_0 = \frac{(p_\mathrm{atm}+kx/S)(h_0+x)}{p_\mathrm{atm}h_0}T_0$

Trabajo en un gas con resorte

De Laplace

1 Enunciado

1.1 Trabajo sobre el gas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES