Compresión adiabática de un gas por un peso
De Laplace
Contenido |
1 Enunciado
Un cilindro vertical de 10.0 cm de diámetro contiene hidrógeno a 25 °C y 100 kPa de presión, que también es la temperatura y presión exterior. La tapa del cilindro puede deslizarse sin rozamiento e inicialmente se encuentra a 10.0 cm de altura. Suponga que las paredes y el émbolo son superficies adiabáticas.
- Se coloca sobre la tapa una pesa de 2.0 kg. Calcule el trabajo realizado sobre el sistema desde el momento que se coloca la pesa hasta el estado de equilibrio final.
- Suponga que en lugar de una pesa se colocan sobre lentamente el émbolo 2.0 kg de arena grano a grano. ¿Cuál es en ese caso el trabajo realizado sobre el sistema?
Para los dos casos anteriores, halle la variación en la energía interna del gas y el calor que entra en el sistema durante el proceso.
2 Introducción
Este problema puede parecer, en una primera inspección, idéntico al del Trabajo en una compresión isoterma por un peso. De hecho, sólo se diferencia en una frase “Suponga que las paredes y el émbolo son superficies adiabáticas”, pero esta frase establece una diferencia esencial. Si el calor puede fluir a través de las paredes, puede alcanzarse el equilibrio térmico con el exterior, la temperatura final en este sistema es la misma que la inicial, la variación de la energía interna es nula, pero no lo es el calor.
En el problema que estamos considerando ahora, en cambio, no puede haber calor atravesando las paredes. Esto impide que se llegue al equilibrio térmico con el exterior; la temperatura final no será la misma que la final, la energía interna cambia durante el proceso, mientras que el calor es nulo.
La ecuación básica para determinar el estado final es el primer principio de la termodinámica
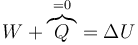
Se trata de calcular por separado el trabajo realizado y la variación en la energía interna para llegar una ecuación que nos permita calcular la temperatura y el volumen final.
Físicamente, lo que ocurre en este caso es que la compresión del gas mete una cantidad energía en el sistema que no puede escapar por ningún sitio, resultando en el calentamiento del hidrógeno.
3 Compresión por una pesa
Al tratarse de una cantidad fija de un gas ideal, se verifica la ecuación de estado
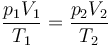
donde, como en el caso isotermo

pero ahora
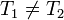
por lo que no puede eliminarse de la ecuación.
Por ser la presión externa constante durante la compresión, el trabajo realizado sobre el gas vale
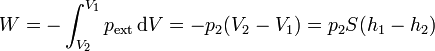
La variación de la energía interna se debe al cambio en la temperatura
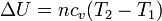
siendo n el número de moles del gas y cv la capacidad calorífica molar a volumen constante. En el caso de un gas diatómico, como el hidrógeno, esta capacidad vale
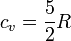
Más en general, la capacidad calorífica a volumen constante se escribe
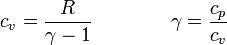
siendo 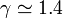 para el hidrógeno. Esta relación da el incremento en la energía
para el hidrógeno. Esta relación da el incremento en la energía
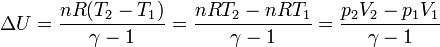
Al ser el proceso adiabático igualamos el trabajo a la variación de la energía interna
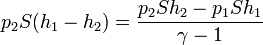
esta ecuación nos permite hallar la altura final del pistón

El valor numérico de la altura final es, sustituyendo los datos del enunciado
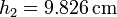
Vemos que se comprime menos que en el caso isotermo (donde bajaba hasta 9.75 cm). La razón es que al calentarse el gas aumenta más rápidamente la presión y por tanto se alcanza antes el equilibrio mecánico.
El trabajo realizado en este proceso es
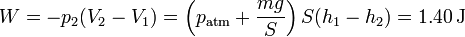
Este trabajo es igual a la variación de la energía interna. La temperatura final de gas vale
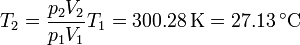
El calor transferido en el proceso es nulo, por ser éste adiabático
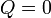
4 Compresión por un montón de arena
En el caso de la compresión gradual, el razonamiento es el mismo que en el caso anterior, y además se aplica a todos y cada uno de los granos de arena que se van añadiendo.
Supongamos que en un cierto momento ya se ha depositado parte de la masa en y en ese instante la presión externa tiene un valor pext (que será intermedio entre p1 y p2). Puesto que el proceso es cuasiestático, esta presión será igual a la interior, por estar el sistema en equilibrio mecánico en todo momento. Si se incrementa la presión en una pequeña cantidad dp el volumen disminuirá de manera diferencial, dV. El trabajo realizado en esta compresión diferencial será
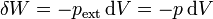
Este trabajo provoca un aumento de la energía interna, que se manifiesta como un aumento de la temperatura
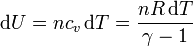
Igualando el trabajo al aumento de la energía interna

Por tratarse de una masa fija de gas se cumple en todo momento
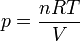
lo que nos da la relación entre diferenciales

Sumando los sucesivos incrementos (integrando)
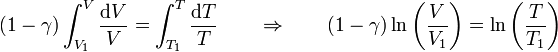
y hallando las exponenciales hallamos la relación entre temperaturas y volúmenes para todo el proceso
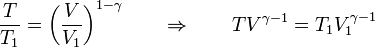
Llevando esto a la ecuación de los gases ideales nos queda la relación entre la presión y el volumen
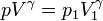
que nos dice que en un proceso adiabático cuasiestático, la presión y el volumen se relacionan un caso particular de proceso politrópico.
Otra forma de llegar a este resultado es observar que en el caso de una pesa de masa finita se cumple
V_2 La posición final del émbolo la obtenemos despejando el volumen final
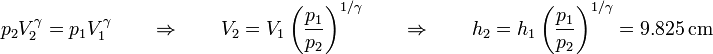
El trabajo que se realiza en el proceso completo es entonces

Con la precisión que estamos trabajando obtenemos el mismo resultado que en el caso anterior. Sin embargo, puesto que V2 es ligeramente mayor, este trabajo es un poco más grande que en el caso de la pesa.
La variación de la energía será igual al trabajo, por ser nulo el calor
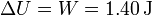
En cuanto a la temperatura final del gas tenemos la ley
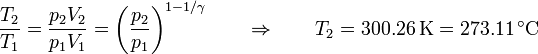
que es ligeramente más baja que en el caso anterior.





