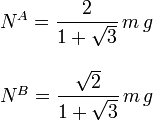Varilla apoyada sobre dos rampas, Enero 2012 (G.I.C.)
De Laplace
Contenido |
1 Enunciado
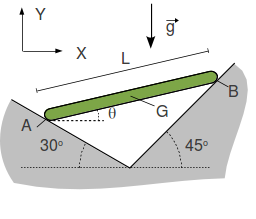
Una barra de longitud L y masa m se apoya sobre dos planos inclinados como se indica en la figura. Los apoyos en los planos son lisos. El peso de la barra se aplica en su centro. Dibuja el diagrama de cuerpo libre de la barra.
- Calcula las fuerzas de reacción vincular en los apoyos (puntos A y B).
- Calcula el valor del ángulo θ para el que la barra se encuentra en equilibrio.
- Consideramos ahora una situación en la que el ángulo θ vale
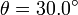 . En este caso el contacto en A es rugoso mientras que en B es liso. Calcula el valor del módulo de la fuerza de rozamiento en A si la masa de la barra es
. En este caso el contacto en A es rugoso mientras que en B es liso. Calcula el valor del módulo de la fuerza de rozamiento en A si la masa de la barra es 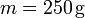 .
.
2 Solución
2.1 Diagrama de sólido libre
Las fuerzas externas que actúan sobre la barra son su peso, aplicado en el centro, y las fuerzas de reacción vincular en los puntos A y B.
Al ser los vínculos lisos, las fuerzas de reacción vincular en los puntos A y B son perpendiculares a las superficies respectivas. Por tanto, 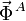 forma un ángulo de
forma un ángulo de 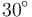 grados con la vertical y la fuerza
grados con la vertical y la fuerza 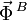 forma un ángulo de
forma un ángulo de 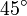 grados con la vertical.
grados con la vertical.
2.2 Fuerzas de reacción vincular
Escogiendo el sentido indicado en el diagrama de sólido libre del apartado anterior, las expresiones en el sistema de ejes indicado de las fuerzas que actúan sobre la barra son
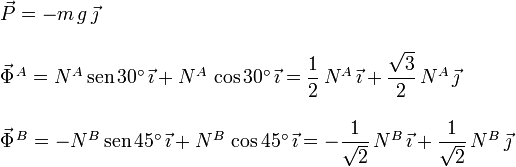
Para que la barra esté en equilibrio la fuerza neta que actúa sobre ella debe ser cero

Igualando las componentes obtenemos dos ecuaciones
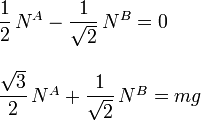
Las incógnitas aquí son NA y NB. Resolviendo el sistema obtenemos las fuerzas de reacción vincular