Los gases ideales (GIE)

De Laplace

Revisión a fecha de 22:11 27 ene 2012; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Introducción
2 Presión y temperatura de un gas
3 Ecuación de estado
4 Gases no ideales. Compresibilidad
5 Trabajo, calor y energía
6 Coeficientes termodinámicos
7 Entropía de un gas ideal

1 Introducción

2 Presión y temperatura de un gas

3 Ecuación de estado

3.1 Ley de Boyle

La ley de Boyle (también conocida como ley de Boyle y Mariotte), nos dice que si en un gas ideal se mantiene la temperatura constante, la presión del gas es inversamente proporcional al volumen que ocupa, lo que se expresa

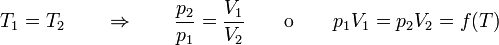
$T_1 = T_2\qquad\Rightarrow\qquad \frac{p_2}{p_1}=\frac{V_1}{V_2}\qquad \mbox{o}\qquad p_1V_1 = p_2V_2=f(T)$

Si aquí introducimos magnitudes específicas, dividiendo por la masa de gas, nos queda

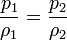
$\frac{p_1}{\rho_1} = \frac{p_2}{\rho_2}$

o, equivalentemente, que la densidad de un gas ideal es proporcional a su presión, a temperatura constante

$p = f(T)\rho\qquad\qquad pV = F(T)$

con $F (T)$ una cierta función de la temperatura y proporcional a la masa de gas.

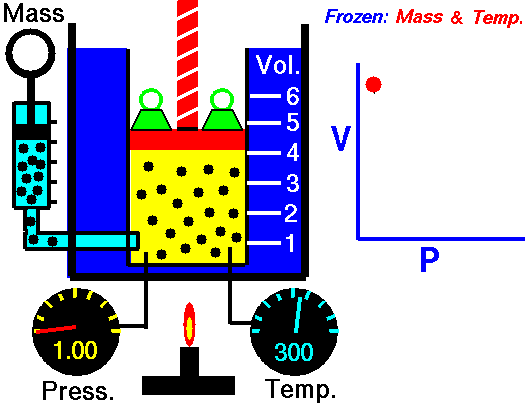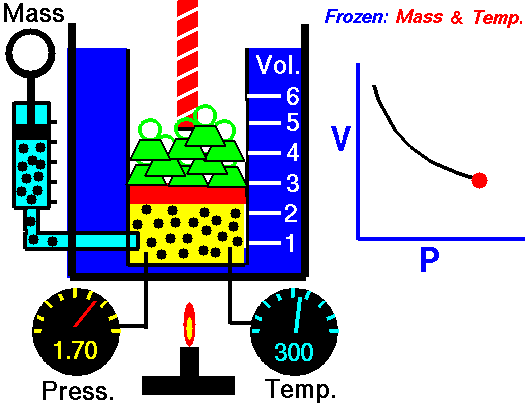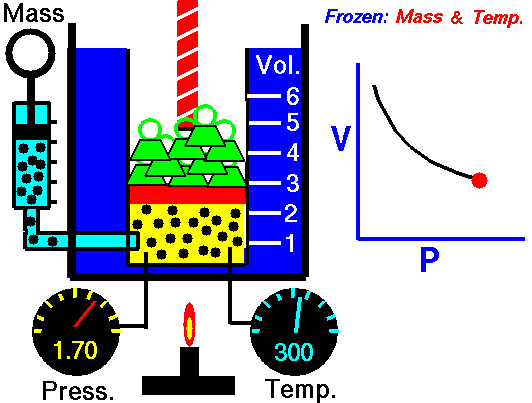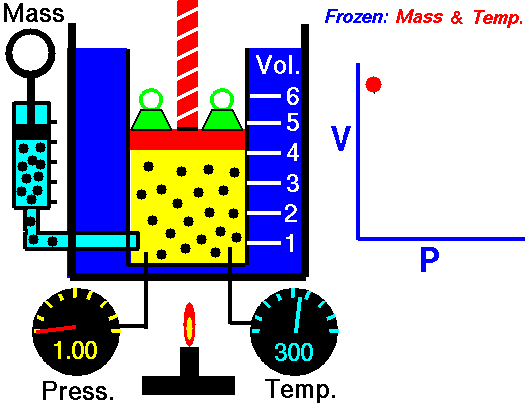
3.2 Ley de Charles

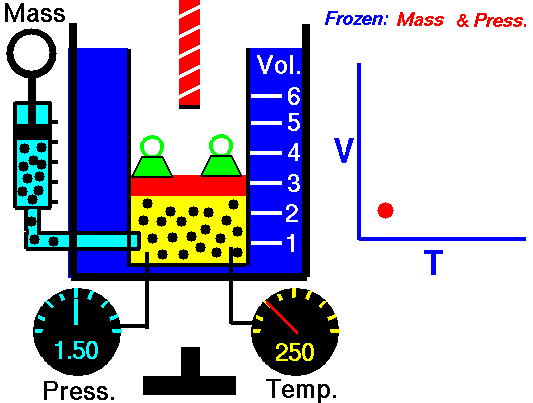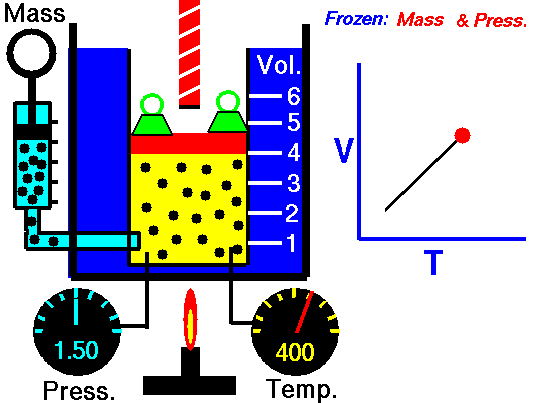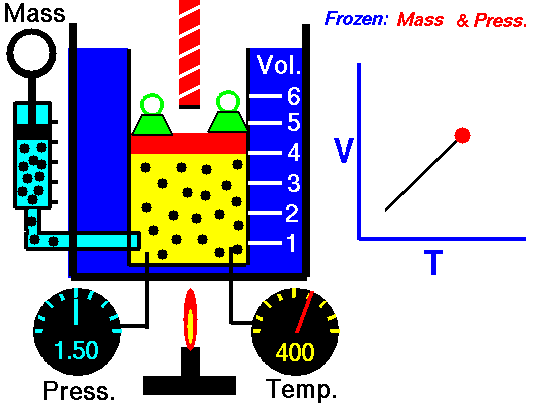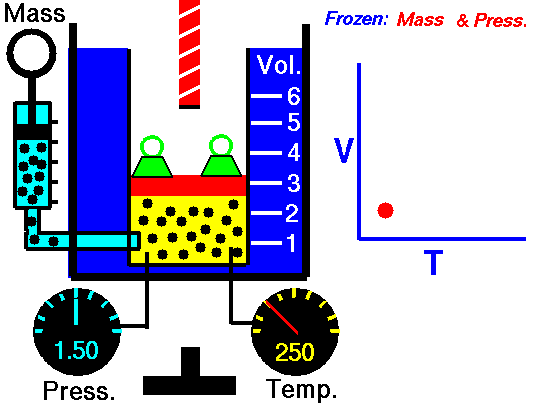
La ley de Charles (también llamada de Gay-Lussac, de Charles y Gay-Lussac, o de los volúmenes) afirma que en un gas ideal a presión constante, el volumen que ocupa el gas varía linealmente con la temperatura que tiene

$p_1=p_2\qquad\Rightarrow\qquad V(t) = A + B t$

o equivalentemente, que la temperatura de un gas ideal varía linealmente con el volumen que ocupa

t = t 0 + k V

Experimentalmente se encuentra que la la ordenada $t 0$ , que representaría la temperatura a la cual el gas ideal ocuparía un volumen nulo (aunque ningún gas se puede llevar hasta esa temperatura), es independiente de la presión del gas siempre que sea baja y vale aproximadamente 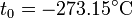$t_0=-273.15^\circ\mathrm{C}$ . Definiendo entonces la temperatura absoluta del gas como

$T = t - t_0 = t+273.15\,^\circ\mathrm{C}$

la ley de Charles se escribe

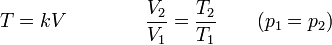
$T = kV\qquad\qquad\frac{V_2}{V_1}=\frac{T_2}{T_1}\qquad (p_1=p_2)$

3.3 Ecuación general

Combinando la ley de Charles con la de Boyle obtenemos

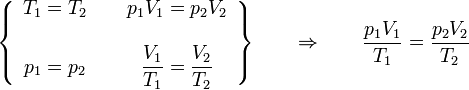
$\left\{\begin{array}{ccc}T_1=T_2&\ & p_1V_1=p_2V_2 \\ && \\ p_1=p_2 & \ & \displaystyle\frac{V_1}{T_1}=\displaystyle \frac{V_2}{T_2}\end{array}\right\}\qquad\Rightarrow\qquad \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}$

o, equivalentemente,

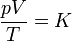
$\frac{pV}{T}=K$

siendo K una constante específica para cada muestra de gas y que no depende ni de la presión, ni del volumen, ni de la temperatura. Puesto que el miembro es una cantidad extensiva (el volumen es proporcional a la masa), el segundo miembro también debe serlo, por lo que puede escribirse en la forma

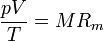
$\frac{pV}{T}=MR_m$

siendo $R m$ una constante diferente para cada gas.

Se encuentra experimentalmente que si en lugar de emplear la masa usamos el número de moles, esta ecuación queda

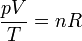
$\frac{pV}{T}=nR$

siendo $R$ una constante que no depende del gas del que se trate. A esta cantidad se la denomina constante de los gases ideales y su valor en el SI es

$R = 8.314\,4621(75)\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}\simeq 8.31\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}$

Esta ecuación de estado suele escribirse en la forma

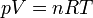
$pV = nRT\,$

3.4 Aplicaciones. Termómetro a volumen constante

4 Gases no ideales. Compresibilidad

5 Trabajo, calor y energía

Como todo sistema termodinámico, sobre un gas se puede realizar trabajo e introducir calor, variando su energía interna

5.1 Trabajo

El trabajo sobre un gas se realiza variando el volumen que ocupa. Consideremos un cilindro con un pistón de área $S$ . Cuando sobre este pistón se ejerce una fuerza normal $F$ el pistón se desplaza una cantidad $d x$ . En este proceso se realiza un trabajo diferencial

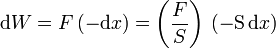
$\mathrm{d}W=F\,(-\mathrm{d}x) = \left(\frac{F}{S}\right)\,(-\mathrm{S}\,\mathrm{d}x)$

El signo negativo en $- d x$ se debe a que el trabajo realizado sobre el gas es positivo cuando el gas se comprime y el émbolo se desplaza hacia el interior del gas. En la última ecuación el primer factor es la presión ejercida sobre el émbolo, mientras que el segundo es la disminución de volumen del gas. Por tanto, el trabajo diferencial es igual a

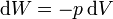
$\mathrm{d}W=-p\,\mathrm{d}V$

Hay que destacar que en esta expresión $p$ es la presión exterior, no la propia del gas. Sólo en procesos cuasiestáticos en que la presión interior iguala prácticamente a la exterior, se podrá sustituir una por otra.

5.2 Energía interna

En principio, la energía interna de un gas puede depender de su temperatura y de su volumen (por ser dos variables independientes). Sin embargo, Joule descubrió que para un gas aproximadamente ideal, la energía interna no depende del volumen, sino solo de su temperatura.

$U=U(T)\,$

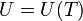
La experiencia de Joule consistió en medir la temperatura de un gas, someterlo a una expansión brusca en el vacío rompiendo un diafragma, y volver a medir la temperatura. Por no haber presión exterior el trabajo es nulo. Por ser una expansión brusca el proceso es prácticamente adiabático y no hay calor transferido al sistema. Por tanto, la energía interna del gas permanece constante

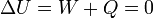
$\Delta U = W + Q = 0\,$

Cuando midió la temperatura final, Joule obtuvo que su valor era prácticamente igual a la inicial. Puesto que la temperatura no cambia, pero el volumen sí, y resulta que la energía interna permanece constante, se llega a la conclusión de que U no depende del volumen y sólo es función de la temperatura.

5.3 Procesos en un gas ideal

5.3.1 Isócoros

5.3.2 Isóbaros

5.3.3 Isotermos

5.3.4 Adiabáticos

6 Coeficientes termodinámicos

7 Entropía de un gas ideal