Ejercicio de dinámica del punto material, Enero 2012
De Laplace
Contenido |
1 Enunciado
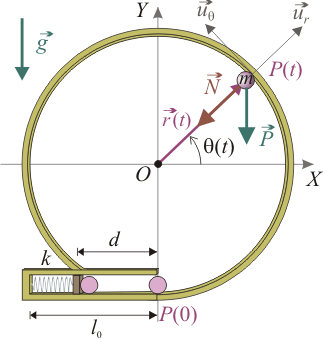
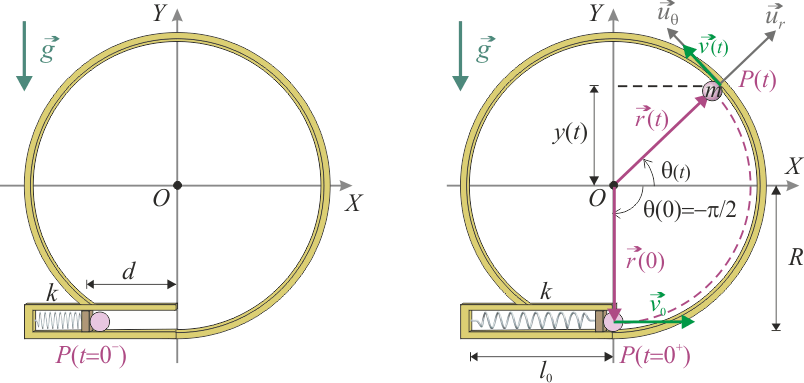
Un partícula P de masa m se desplaza por la cara interior de un aro fijo de radio R y centro O dispuesto en el plano vertical OXY, de manera que la posición de la partícula viene determinada en cada instante por el correspondiente valor del ángulo θ indicado en la figura. En el instante inicial la partÍcula se encuentra en la posición θ(0) = − π / 2, tras ser lanzada por un disparador consistente en un resorte de longitud natural l0 y constante recuperadora k, que previamente había sido comprimido una distancia d.Nada impide que la partícula pueda separarse del aro, pero cuando están en contacto el rozamiento entre ambos cuerpos es despreciable. Por tanto, la correspondiente fuerza de reacción vincular puede expresarse en la base de las coordenadas polares 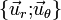 , como
, como 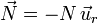 .
.
- Diagrama de fuerzas y descripción.
- Ecuaciones de movimiento.
- Energía mecánica del sistema.
- Momento cinético de la partícula.
2 Solución
2.1 Diagrama de fuerzas y descripción
En el enunciado del ejercicio se incluye una figura donde se indica el diagrama de fuerzas que actúan sobre la partícula, e incluso se describe de forma explícita cómo es la fuerza de reacción vincular que modela el contacto aro-partícula. Comenzaremos con una descripción detallada de dichas fuerzas. Para describirlas analíticamente podemos utilizar el sistema de referencia cartesiano indicado en la figura del enunciado: el plano OXY está definido por el plano fijo que contiene al aro, siendo su centro O el origen del sistema de referencia, y con la dirección OY en la vertical gravitatoria, pero con sentido opuesto.
Sin embargo, si la partícula material se va a mover en contacto con el aro (es decir, sobre la curva Γ indicada en la figura) el sistema de referencia 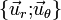 de las coordenadas polares resulta mucho más útil para describir, tanto la fuerza de reacción vincular, como las magnitudes cienmáticas de la partícula. Como se sabe, dicho sistema de coordenadas describe la posición de la partícula en el plano Π:z = 0 (es decir, el plano OXY), en términos de la distancia r al origen O, y del ángulo θ que forma el radio vector
de las coordenadas polares resulta mucho más útil para describir, tanto la fuerza de reacción vincular, como las magnitudes cienmáticas de la partícula. Como se sabe, dicho sistema de coordenadas describe la posición de la partícula en el plano Π:z = 0 (es decir, el plano OXY), en términos de la distancia r al origen O, y del ángulo θ que forma el radio vector 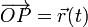 con la dirección adoptada como eje OX: P = P(r,θ). Como hemos tomado el origen del sistema de referencia en el centro del aro, si la partícula se mueve en contacto con la cara interior de aro, se mantendrá a una distancia constante r = R, de manera que:
con la dirección adoptada como eje OX: P = P(r,θ). Como hemos tomado el origen del sistema de referencia en el centro del aro, si la partícula se mueve en contacto con la cara interior de aro, se mantendrá a una distancia constante r = R, de manera que:
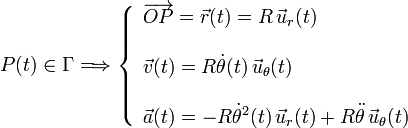
Consideremos que nos encontramos en un instante posterior al lanzamiento, en el cuál la partícula material ocupa la posición P(t) = P[R,θ(t)]. Estará sometida, por tanto, a una fuerza vincular  que modela el contacto con el aro. Si en dicho contacto no hay rozamiento, la fuerza vincular se limitará a impedir los desplazamientos no compatibles con el vínculo.
que modela el contacto con el aro. Si en dicho contacto no hay rozamiento, la fuerza vincular se limitará a impedir los desplazamientos no compatibles con el vínculo.
Obsérvese que si la partícula estuviese obligada a recorrer la trayectoria Γ su único desplazamiento permitido sería tangente a dicha curva y, por tanto, colineal con 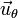 en cada punto. Sin embargo, nada obliga a que el punto material permanezca siempre en contacto con la cara interior del aro, pudiendo llegar a despegarse de él. Lo que no está permitido es que la partícula P se desplace aumentando su distancia respecto del punto O. Así, la expresión analítica del desplazamiento virtual compatible con dicho contacto unilateral será:
en cada punto. Sin embargo, nada obliga a que el punto material permanezca siempre en contacto con la cara interior del aro, pudiendo llegar a despegarse de él. Lo que no está permitido es que la partícula P se desplace aumentando su distancia respecto del punto O. Así, la expresión analítica del desplazamiento virtual compatible con dicho contacto unilateral será:
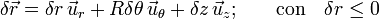
Aplicamos ahora el principio de liberación, considerando que la fuerza vincular sólo actúa para impedir desplazamientos no compatibles, los cuáles se corresponderían con variaciones δr > 0. Se tendrá, por tanto,
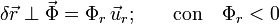
Es decir, si la partícula está en contacto con el aro, sobre aquélla actuará una fuerza de reacción vincular que actúa en la dirección del vector 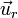 , pero en sentido contrario. Esta fuerza vincular es, al fin y al cabo, la reacción normal del aro; por tanto, podemos denotarla de la siguiente forma:
, pero en sentido contrario. Esta fuerza vincular es, al fin y al cabo, la reacción normal del aro; por tanto, podemos denotarla de la siguiente forma:
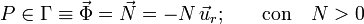
Por otra parte, como se trata de una partícula pesada en el campo gravitatorio terrestre, estará sometida a la fuerza peso  , que también expresaremos en la base de las coordenadas polares. Teniendo en cuenta que, en la posición arbitraria indicada en la figura, la vertical gravitatoria forma un ángulo θ con la dirección del vector
, que también expresaremos en la base de las coordenadas polares. Teniendo en cuenta que, en la posición arbitraria indicada en la figura, la vertical gravitatoria forma un ángulo θ con la dirección del vector 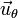 , se tendra:
, se tendra:
![\vec{P}=m\!\ \vec{g}=-mg\!\ \big[\mathrm{sen}\!\ \theta\!\ \vec{u}_r(t)+\cos\theta\!\ \vec{u}_\theta(t)\big]](/wiki/images/math/f/1/5/f1541134a67698be227de3a1862b3980.png)
2.2 Ecuaciones de movimiento para la partícula
2.2.1 En contacto con el aro
Las leyes de la dinámica permiten establecer las ecuaciones diferenciales que describen las propiedades del movimiento de la partícula en función de las causas (fuerzas) que lo producen o condicionan. Si la partícula está en contacto con el aro, sobre aquélla actúan simultáneamente la fuerza peso y la reacción vincular discutida en el apartado anterior. El producto de la masa por la aceleración instantánea de la partícula es igual al valor de la resultante de dichas fuerzas en la posición P[R,θ(t)] ocupada por el punto material en un ese instante:
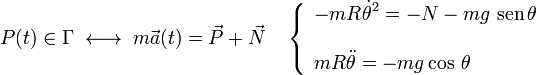
Es decir, al proyectar la ecuación vectorial en las direcciones definidas por los vectores de la base de polares se obtienen sendas ecuaciones diferenciales escalares: la integración de la correspondiente a la dirección 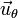 proporciona la ley horaria θ(t) que describe la evolución de la posición de la partícula en contacto con el aro. Por su parte, la ecuación en la dirección radial
proporciona la ley horaria θ(t) que describe la evolución de la posición de la partícula en contacto con el aro. Por su parte, la ecuación en la dirección radial 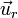 permite determinar la componente de la fuerza de reacción normal en función de la posición ocupada por la partícula en el aro y de su velocidad en un determinado instante.
permite determinar la componente de la fuerza de reacción normal en función de la posición ocupada por la partícula en el aro y de su velocidad en un determinado instante.
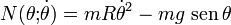
Obsérvese que, exigiendo en esta ecuación que el valor de la reacción vincular N sea estrictamente positivo, podemos discriminar si la partícula está o no en contacto con la cara interior del aro, en función de su posición y velocidad:
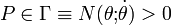
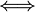
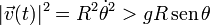
Por otra parte, a raíz de la discusión realizada en el apartado anterior sobre el vínculo existente en el contacto partícula-aro, quedaría una cuestión pendiente: allí admitimos que dicho contacto no impide un virtual desplazamiento de la partícula 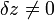 en la dirección perpendicular al plano OXY. Como las fuerzas que actúan sobre la partícula no tienen componente en esa dirección, la correspondiente componente de la aceleración sería nula:
en la dirección perpendicular al plano OXY. Como las fuerzas que actúan sobre la partícula no tienen componente en esa dirección, la correspondiente componente de la aceleración sería nula:
![\forall\, t\mathrm{,}\quad \vec{k}\cdot\big[m\vec{a}(t)\big]=m\ddot{z}=0\qquad\longrightarrow\qquad z(t)=\dot{z}(0)\!\ t+z(0)](/wiki/images/math/a/f/6/af6e90f3fb29588247a8531908c008fa.png)
En consecuencia, si la partícula sale del disparador (situado en el plano Π:z = 0) con una velocidad inicial que no tiene componente en la dirección perpendicular al plano vertical OXY, aquélla se moverá siempre contenida en dicho plano:
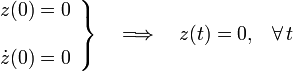
2.2.2 En caso de pérdida del contacto
Consideremos el caso en que, tras desplazarse por la cara interior del aro durante un intervalo de tiempo, la partícula deja de estar en contacto con el aro en el instante td. La posición y velocidad de la partícula en dicho instante deben ser tales que se anule el valor de la reacción normal del aro; es decir,
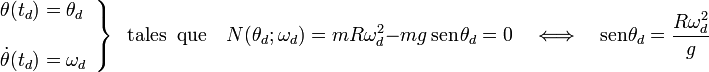
Una previsible consecuencia de este resultado es que la partícula sólo se podría separar del aro en el rango de posiciones correspondiente al intervalo 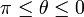 .
.
Tras perderse el contacto, sobre la partícula sólo actuaría la fuerza peso, por lo que la aceleración de la partícula sería la gravitatoria, constante en dirección módulo y sentido:
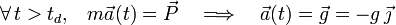
Tal como puede comprobarse en el ejercicio dedicado al estudio cinemático de una partícula bajo la acción exclusiva del campo gravitatorio terrestre, las ecuaciones horarias que describen el movimiento de la partícula a partir del instante td serán:
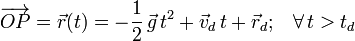
donde 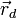 y
y 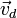 son los vectores que indican la posición y velocidad de la partícula en el instante en que pierde el contacto con el disco. Es decir,
son los vectores que indican la posición y velocidad de la partícula en el instante en que pierde el contacto con el disco. Es decir,
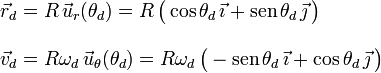
2.3 Energía mecánica del sistema
2.3.1 Aplicación del teorema de la energía cinética
El teorema de las "fuerzas vivas" o de la energía cinética para una partícula material establece que el trabajo resultante realizado en cada instante de tiempo por todas las fuerzas 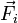 que actúan sobre la partícula es igual a la variación de su energía cinética:
que actúan sobre la partícula es igual a la variación de su energía cinética:
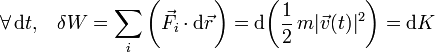
siendo 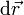 el desplazamiento sufrido por la partícula en dicho intervalo infitesimal de tiempo.
el desplazamiento sufrido por la partícula en dicho intervalo infitesimal de tiempo.
Como hemos visto anterioremente, en el ejercicio que nos ocupa pueden darse dos situaciones a las que corresponden dos sistemas de fuerzas distintos actuando sobre la partícula: si la partícula está en contacto con el aro, sobre aquélla ejercen su acción la fuerza peso  y la fuerza de reacción vincular
y la fuerza de reacción vincular  ; si la partícula llega a perder el contacto con el aro, sólo actuará el peso.
; si la partícula llega a perder el contacto con el aro, sólo actuará el peso.
Si, hallándose el sistema en la primera situación descrita, la partícula sufre un desplazamiento manteniendo el contacto con el aro, se tendrá que:
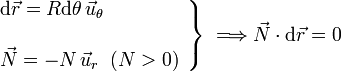
Por otra parte, si el desplazamiento 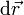 tuviese una componente en la dirección radial significaría que la partícula se ha despegado del aro anulándose, por tanto, el valor de la reacción normal N. En consecuencia, tenemos que la fuerza de reacción vincular
tuviese una componente en la dirección radial significaría que la partícula se ha despegado del aro anulándose, por tanto, el valor de la reacción normal N. En consecuencia, tenemos que la fuerza de reacción vincular  nunca va a realizar trabajo. Es decir, el peso va a ser la única fuerza que realiza trabajo sobre la partícula modificando su energía cinética, tanto en el caso de que la partícula se mueva en contacto con el aro (vínculo unilateral liso), como si se despega y mueve libremente:
nunca va a realizar trabajo. Es decir, el peso va a ser la única fuerza que realiza trabajo sobre la partícula modificando su energía cinética, tanto en el caso de que la partícula se mueva en contacto con el aro (vínculo unilateral liso), como si se despega y mueve libremente:
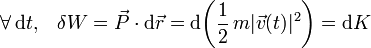
2.3.2 Energía potencial. Conservación de la energía mecánica
Pero, como sabemos, el peso es una fuerza conservativa. Es decir, el trabajo que realiza cuando la partícula P se desplaza depende sólo de las posiciones inicial y final, por lo que se puede definir una energía potencial gravitatoria 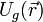 , tal que:
, tal que:
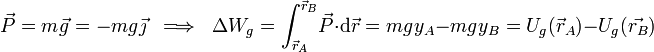
Por tanto, el valor de la energía potencial gravitatoria de la partícula está determinado por su coordenada “Textoy”. Existe también una constante de integración U0, cuyo valor depende de donde fijemos (arbitrariamente) el origen de potencia. Si tomamos éste en el plano y = 0 tendremos que...
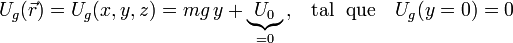
Como vimos en el subapartado anterior, el peso es la única fuerza que realiza trabajo, cualquiera que sea la trayectoria seguida por la partícula. Por tanto, se tendrá que:
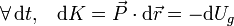
Si aplicamos ahora la definición de la energía mecánica de la partícula como la suma de la energía cinética más las energías potenciales de las fuerzas conservativas que actúan sobre ella,
![E(t)=K(t)+U_g\big[\vec{r}(t)\big]\mathrm{,}](/wiki/images/math/7/9/a/79a996cc84043e074daa38727a228e4c.png)
y teniendo en cuenta el resultado anterior, llegamos a la siguiente conclusión:
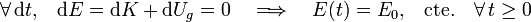
Es decir, tras ser lanzada desde el disparador en el instante inicial (t = 0), la energía mecánica de la partícula tendrá un valor constante E0, independientemente de la trayectoria que siga (en contacto con el aro o separándose de él).
2.3.3 Cálculo del valor de la energía mecánica
El valor de dicha constante lo determinaremos calculando la energía mecánica de la partícula en el instante t = 0 + , inmediatamente posterior al momento en que la partícula sale del resorte con una velocidad 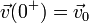 . Como el resorte se encuentra en el plano y = − R, tendremos que...
. Como el resorte se encuentra en el plano y = − R, tendremos que...
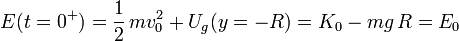
Y para calcular el valor de la energía cinética inicial, K0, analizaremos el proceso de disparo. Consideraremos que éste proceso ocurre de forma prácticamente instantánea en t = 0. Además, podríamos simplificar el análisis considerando que se trata de un proceso ideal (o casi ideal) en el cuál no hay pérdidas apreciables de energía por fenómenos de fricción y/o deformación de los cuerpos. De esta manera, la energía mecánica del sistema -y por tanto de la partícula, al despreciar el valor de la masa del resorte- permanecería constante durante el disparo. Sin embargo, podemos ser más realistas en nuestras consideraciones y admitir la posibilidad de que en el proceso de disparo puediera haber una cierta disipación de energía. Esto supondría que, entre los instantes inmediatamente anterior (t = 0 − ) y posterior (t = 0 + ) al momento del disparo, el incremento de la energía mecánica de la partícula debe ser negativo, o despreciable en el mejor de los casos. Descomponiendo dicho incremento como la suma de las variaciones de las energía cinética y potencial, obtenemos la siguiente inecuación que describe el balance energético en el proceso de disparo:
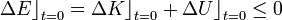
Como la partícula estaba en reposo el antes de ser disparada, el incremento sufrido por su energía cinética será:
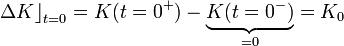
Y como el disparador se encuentra en el plano y = − R, la variación de energía potencial en t = 0 se deberá exclusivamente al cambio de la energía 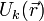 del resorte al pasar de estar comprimido una distancia d en t = 0 − , a recuperar su longitud natural en t = 0 + :
del resorte al pasar de estar comprimido una distancia d en t = 0 − , a recuperar su longitud natural en t = 0 + :
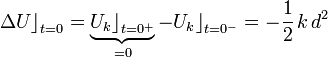
Aplicando ahora la inecuación resultante del balance energético en el proceso de disparo, obtenemos una cota superior para el valor constante que va a tener la enería mecánica de la partícula una vez lanzada:
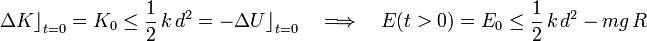
2.3.4 Condiciones para que la partícula complete una vuelta
Obtengamos la expresión de las energías cinética y potencial de la partícula, en función de su posición y velocidad, cuando se desplaza en contacto con el aro:
![P(t)\in\Gamma\;\Longrightarrow\;\left\{\begin{array}{l}\vec{r}(t)=R\!\ \vec{u}_r=R\left[\cos\theta(t)\!\ \vec{\imath}+\mathrm{sen}\!\ \theta (t)\vec{\jmath}\!\ \right]\\ \\ \vec{v}(t)=R\!\ \dot{\theta}(t)\vec{u}_\theta[\theta(t)]\end{array}\right\}\;\Longrightarrow](/wiki/images/math/f/7/1/f71c6b0bdd296edee93aa1acb31d7b5d.png)
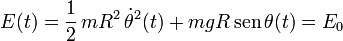
Si exigimos la condición requerida a la velocidad de la partícula para que ésta se halle en contacto con la cara interior del aro en una posición dada por un determinado valor del ángulo θ, obtenemos una inecuación que indica el valor minímo que debe tener la energía mecánica de la partícula para que pueda alcanzar dicha posición.
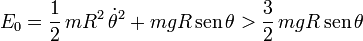
Para que la partícula efectúe una vuelta completa es necesario que el valor de E0 verifique la inecuación anterior para todo valor del ángulo θ, incluida la posición correspondiente a θ = π / 2, en la cuál la energía potencial gravitatoria de la partícula (en contacto con el aro) alcanza su valor máximo:
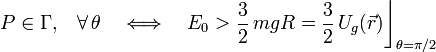
Teniendo en cuenta ahora la relación de la distancia d de compresión del resorte con la energía mecánica de la partícula (apartado 2.3.3), obtenemos una estimación del valor mínimo que ha de tener dicha distancia para que la partícula pueda completar una vuelta en contacto con la cara interior del aro:
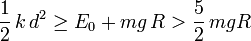
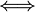
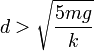
2.4 Momento cinético de la partícula
El momento cinético  de una partícula P respecto de un punto de referencia O se define como el momento del vector cantidad de movimiento respecto de dicho punto. Y si éste es el origen del sistema de referencia utilizado para describir la posición de la partícula, se tendrá que:
de una partícula P respecto de un punto de referencia O se define como el momento del vector cantidad de movimiento respecto de dicho punto. Y si éste es el origen del sistema de referencia utilizado para describir la posición de la partícula, se tendrá que:
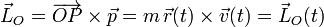
Se trata, por tanto, de una magnitud física variable en el tiempo, cuya variación instantánea es igual a la resultante de los momentos de las fuerzas aplicadas sobre la partícula (teorema del momento cinético):
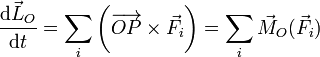
Como ya se ha discutido, la partícula del sistema bajo estudio puede estar sometida a dos sistemas de fuerzas distintos: la fuerza peso y la reacción vincular del aro sobre aquélla, si ambos están en contacto; y sólo la fuerza peso si la partícula se ha separado del aro.
Obsérvese que el momento respecto de O de la fuerza de reacción vincular  va a ser siempre nulo ya que, si existe tal fuerza es porque la partícula está en contacto con el aro, y en esta situación los vectores
va a ser siempre nulo ya que, si existe tal fuerza es porque la partícula está en contacto con el aro, y en esta situación los vectores  y
y  son colineales:
son colineales:
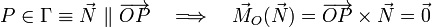
Consecuentemente, la variación instantánea del momento cinético de la partícula respecto del punto O será debida a la acción exclusiva de la fuerza peso, independientemente de la trayectoria seguida por aquélla:
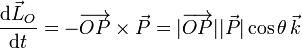
siendo θ el ángulo formado por el radiovector posición 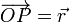 y la dirección horizontal OX.
y la dirección horizontal OX.
En el caso particular de que la partícula se mueva por en contacto con el aro, su momento cinético respecto de O y la derivada temporal de éste son:
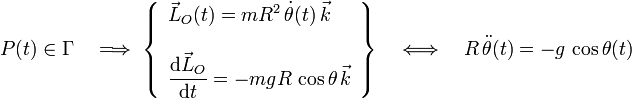
Nótese que este último resultado es la misma ecuación de movimiento que obtuvimos en el apartado 2.2.1.