Ejemplo de armadura simple, Enero 2012 (G.I.C.)

De Laplace

Revisión a fecha de 10:42 24 ene 2012; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución
- 2.1 Reacciones en los apoyos
- 2.2 Tensión en la barra BC

1 Enunciado

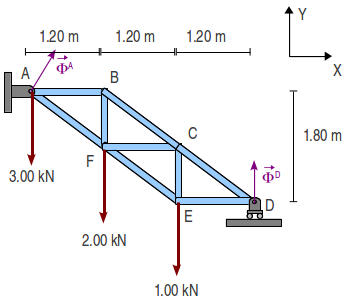
Se tienen la armadura de la figura. Los pesos de las barras son despreciables frente a las cargas.

Calcula las reacciones en los apoyos.
Calcula la tensión en la barra $B C$ .

2 Solución

2.1 Reacciones en los apoyos

Tratamos la armadura como un sólido rígido. Las fuerzas externas son las cargas en los nudos A, F, E y las reacciones en los apoyos A y E. El vínculo en A es una articulación, por lo que la fuerza de reacción vincular puede tener dos componentes. El apoyo en D es de rodillo, es decir, la fuerza de reacción vincular sólo puede tener componente perpendicular a la superficie

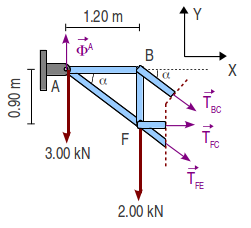
Proyectamos las cargas y las fuerzas de reacción vincular en los ejes de la figura

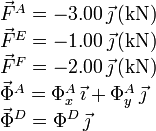
$\begin{array}{l} \vec{F}^A = -3.00\,\vec{\jmath}\, \mathrm{(kN)}\\ \vec{F}^E = -1.00\,\vec{\jmath}\, \mathrm{(kN)}\\ \vec{F}^F = -2.00\,\vec{\jmath}\, \mathrm{(kN)}\\ \vec{\Phi}^A = \Phi^A_x\,\vec{\imath} + \Phi^A_y\,\vec{\jmath}\\ \vec{\Phi}^D = \Phi^D\,\vec{\jmath} \end{array}$

Las condiciones de equilibrio son que la fuerza neta debe anularse y el momento neto debe ser nulo respecto de cualquier punto.

Aplicando que la fuerza neta debe ser cero tenemos

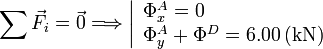
$\sum\vec{F}_i = \vec{0} \Longrightarrow \left| \begin{array}{l} \Phi^A_x = 0\\ \Phi^A_y + \Phi^D = 6.00 \,\mathrm{(kN)} \end{array} \right.$

La otra ecuación se obtiene de imponer que el momento neto es nulo. Escogemos el punto A para calcular el momento. Tenemos

$\begin{array}{l} \vec{M}^A_F = -1.20 \times 2.00 \,\vec{k} = -2.40\,\vec{k} \,(\mathrm{kN\cdot m}) \\ \vec{M}^A_E = -2.40 \times 1.00 \,\vec{k} = -2.40\,\vec{k} \,(\mathrm{kN\cdot m})\\ \vec{M}^A_D = 3.60 \times \Phi^D \,\vec{k} = 3.60 \,\Phi^D\,\vec{k} \end{array}$

El momento de las otras fuerzas es nulo. La suma debe ser cero. De aquí obtenemos

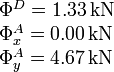
$\begin{array}{l} \Phi^D = 1.33\,\mathrm{kN}\\ \Phi^A_x = 0.00\,\mathrm{kN}\\ \Phi^A_y = 4.67\,\mathrm{kN} \end{array}$

2.2 Tensión en la barra BC

Lo más sencillo es usar el método de las secciones. Dividimos la estructura en dos partes, de modo que la línea de separación corte la barra BC. La figura muestra una posible división. Cada barra seccionada es sustituida por una fuerza dirigida en la dirección de la barra y de magnitud la tensión en ella.

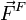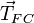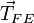La condición de equilibrio es que, en cada parte de la estructura, la suma de fuerzas y de momentos debe ser cero. En este caso, nos basta aplicar que el momento de todas las fuerzas respecto al punto F es cero para obtener una ecuación para $T B C$ . Los momentos respecto a F de las fuerzas $\vec{F}^F$ , $\vec{T}_{FC}$ y $\vec{T}_{FE}$ son nulos, pues el punto F está contenido en sus rectas soporte. 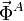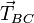Por tanto sólo hay que calcular el momento de las fuerzas $\vec{F}^A$ , $\vec{\Phi}^A$ y $\vec{T}_{BC}$ . En el sistema de ejes de la figura tenemos

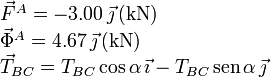
$\begin{array}{l} \vec{F}^A = -3.00\,\vec{\jmath}\,(\mathrm{kN})\\ \vec{\Phi}^A = 4.67\,\vec{\jmath}\,(\mathrm{kN})\\ \vec{T}_{BC} = T_{BC}\cos\alpha\,\vec{\imath}- T_{BC}\,\mathrm{sen}\,\alpha\,\vec{\jmath} \end{array}$

El seno y el coseno del ángulo son

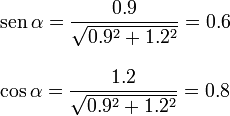
$\begin{array}{l} \mathrm{sen}\,\alpha = \dfrac{0.9}{\sqrt{0.9^2+1.2^2}} = 0.6\\ \\ \cos\alpha = \dfrac{1.2}{\sqrt{0.9^2+1.2^2}} = 0.8 \end{array}$

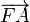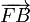Necesitamos los vectores $\overrightarrow{FA}$ y $\overrightarrow{FB}$ para calcular los momentos

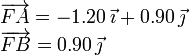
$\begin{array}{l} \overrightarrow{FA} = -1.20\,\vec{\imath} + 0.90\,\vec{\jmath}\\ \overrightarrow{FB} = 0.90\,\vec{\jmath} \end{array}$

Los momentos de las tres fuerzas involucradas son

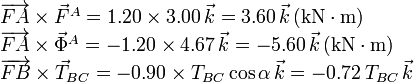
$\begin{array}{l} \overrightarrow{FA}\times\vec{F}^A = 1.20\times3.00\,\vec{k} = 3.60\,\vec{k}\,\mathrm{(kN\cdot m)}\\ \overrightarrow{FA}\times\vec{\Phi}^A = -1.20\times4.67\,\vec{k} = -5.60\,\vec{k}\,\mathrm{(kN\cdot m)}\\ \overrightarrow{FB}\times\vec{T}_{BC} = -0.90\times T_{BC}\cos\alpha\,\vec{k} = -0.72\,T_{BC}\,\vec{k} \end{array}$

La suma de los tres vectores debe ser cero. De ahí obtenemos

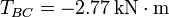
$T_{BC} = -2.77\,\mathrm{kN\cdot m}$

La barra trabaja a compresión.

Ejemplo de armadura simple, Enero 2012 (G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Reacciones en los apoyos

2.2 Tensión en la barra BC

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES