Momento de inercia de un sistema de partículas
De Laplace
Contenido |
1 Enunciado
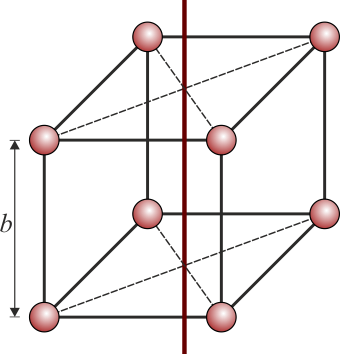
Se tiene un sólido formado por ocho partículas de masa m situadas en los vértices de un cubo de arista a. Halle el momento de inercia del cubo respecto a los siguientes ejes:
- Uno perpendicular a una cara y que pase por el centro del cubo.
- Uno que pase por dos vértices opuestos.
- Uno que pase por los centros de dos aristas opuestas.
- Uno que pase por una arista
2 Introducción
El momento de inercia de un sólido respecto a un eje se define como la suma, para todas las partículas del sólido,
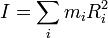
siendo Ri la distancia del punto donde se encuentra la partícula i al eje respecto del cual se calcula el momento de inercia.
El eje se define dando un punto por el que pase, 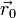 y un vector director
y un vector director  en la dirección de la recta. La distancia de un punto cualquiera al eje puede hallarse como la proyección ortogonal de la posición relativa
en la dirección de la recta. La distancia de un punto cualquiera al eje puede hallarse como la proyección ortogonal de la posición relativa
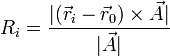
3 Eje por dos caras opuestas
En el primer caso, tenemos un eje que atraviesa dos caras opuestas por su punto central. Este eje pasa también por el centro del cubo.
La distancia de las ocho masas al eje es la misma en todos los casos y vale
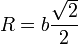
con lo que el momento de inercia del sólido respecto a este eje vale
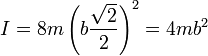
4 Eje por dos vértices opuestos
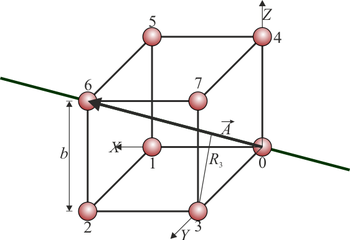
En el segundo caso tenemos un eje que pasa por dos vértices opuestos. Por lo pronto, la distancia de dos de las partículas al eje es nula. Siguiendo el esquema de etiquetas de la figura, sería
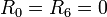
Las otras seis masas se encuentran a la misma distancia del eje. Por la simetría del cuerpo, es claro que la distancia de las masas 1, 3 y 4, que se encuentran en posiciones análogas respecto a la masa 0, se hallan equidistantes del eje. Las masas 2, 5 y 7 no están en la misma posición relativa a la masa 0 que las anteriores, pero sí lo están respecto a la masa 6, por lo que su distancia al eje también es igual. En cualquier caso, el cálculo que sigue puede efectuarse de forma sencilla para cada una de las seis masas.
Consideremos la masa 3. Su vector de posición respecto a la masa 0 es
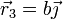
Un vector director de este eje es el que uno los dos vértices por los que pasa
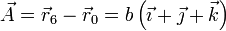
La distancia entre la masa 3 y el eje la da la proyección ortogonal
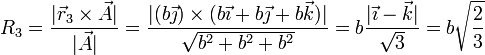
Obsérvese que esta distancia no es igual a la mitad de la diagonal del cubo. El punto del eje a la mínima distancia de la masa no está en el centro del cubo (está a un 1/3 de la diagonal, como se ve si se halla la proyección paralela).
El momento de inercia respecto a este eje vale entonces
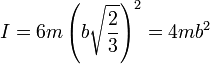
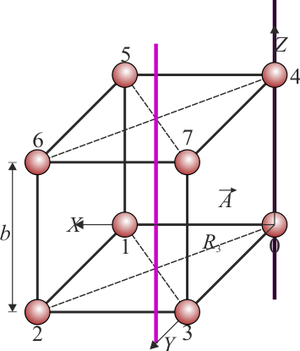
5 Eje por dos aristas opuestas
En el tercer caso, el eje corta dos aristas opuestas. Tenemos ahora dos casos posibles:
- Hay cuatro masas situadas en las aristas por las que pasa el eje. La distancia de cada una de estas masas al eje es media arista
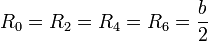
- Las cuatro masas restantes se encuentran sobre un plano que es perpendicular al eje en el centro del cubo. La distancia de cada una de estas masas al eje es media diaagonal del cubo
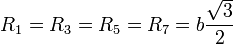
Estos dos cálculos se pueden también hallar empleando la fórmula vectorial aplicada al caso anterior, cambiando los vectores por los correspondientes a este caso.
El momento de inercia respecto a este eje vale entonces
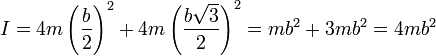
Vemos que en los tres casos obtenemos el mismo momento de inercia. Esto es una propiedad del cubo, que comparte con la esfera, de que cualquiera que sea el eje que se tome, siempre que pase por el centro del cubo, el resultado es el mismo.
6 Eje por una arista
En el último caso el eje no pasa por el centro del cubo, por lo que su valor no será igual al de los tres casos anteriores. Podemos hallar su valor mediante el teorema de Steiner
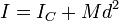
El momento respecto al eje que pasa por el CM ya lo conocemos. La distancia de este nuevo eje respecto al que pasa por el CM es media diagonal de una cara
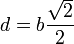
y obtenemos el momento de inercia
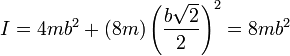
También podemos llegar a este resultado directamente a partir de las distancias de cada una de las partículas al eje. tenemos:
- Dos masas a distancia nula
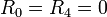
- Cuatro masas a una distancia de una arista
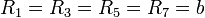
- Dos masas a una distancia de una diagonal de una cara
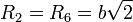
Reuniendo todos los valores obtenemos el momento de inercia
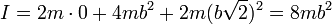
en completo acuerdo con el anterior.