Problemas de Movimiento oscilatorio (GIC)
De Laplace
Contenido |
1 Problemas del boletín
1.1 Pelota que bota y bota
Un balón que se ha dejado caer desde una altura de 4 m choca con el suelo con una colisión perfectamente elástica. Suponiendo que no se pierde energía debido a la resistencia del aire, demuestre que el movimiento es periódico. Determine el periodo del movimiento, ¿Es éste un movimiento armónico simple?
1.2 Solución general del MAS
La solución general de la ecuación de movimiento
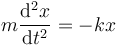
es de la forma
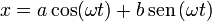
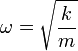
con a y b dos constantes dependientes de las condiciones iniciales.
- Halle el valor de las constantes a y b si la posición inicial de la partícula es x0 y su velocidad inicial es v0.
- Demuestre que la ecuación horaria
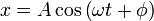 es también solución de la misma ecuación de movimiento. Empleando relaciones trigonométricas, deduzca la relación entre las constantes {A,φ} y las constantes {a,b}. Exprese A y φ en función de la posición y la velocidad iniciales, x0 y v0.
es también solución de la misma ecuación de movimiento. Empleando relaciones trigonométricas, deduzca la relación entre las constantes {A,φ} y las constantes {a,b}. Exprese A y φ en función de la posición y la velocidad iniciales, x0 y v0.
- Calcule la velocidad de la partícula para cualquier instante en función de la posición y velocidad iniciales.
- Demuestre que la cantidad E = mv2 / 2 + kx2 / 2 no depende del tiempo. ¿Cuánto vale en función de las condiciones iniciales?
- Demuestre que x = ejωt, con
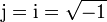 , la unidad imaginaria, es una solución particular de la ecuación de movimiento. Aplicando los resultados anteriores, demuestre la relación
, la unidad imaginaria, es una solución particular de la ecuación de movimiento. Aplicando los resultados anteriores, demuestre la relación
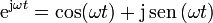
1.3 Masa de un astronauta
Para medir la masa de un astronauta en ausencia de gravedad se emplea un aparato medidor de masa corporal. Este aparato consiste, básicamente, en una silla que oscila en contacto con un resorte. El astronauta ha de medir su periodo de oscilación en la silla. En la segunda misión Skylab el resorte empleado tenía una constante k = 605.6 N/m y el periodo de oscilación de la silla vacía era de 0.90149 s. Calcule la masa de la silla. Con un astronauta en la silla el periodo medido fue 2.08832 s. Calcule la masa del astronauta.
1.4 Oscilador amortiguado
Un oscilador amortiguado experimenta una fuerza de rozamiento viscoso 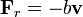 , de forma que su ecuación de movimiento, para un movimiento unidimensional es
, de forma que su ecuación de movimiento, para un movimiento unidimensional es
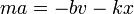
- Demuestre que la energía mecánica
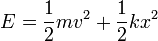
- Si buscamos una solución particular de la forma x = Aeλt, calcule los dos valores que puede tener λ. La solución general será una combinación de las dos posibilidades:
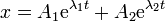
- ¿Cuál es el máximo valor de b para que haya oscilaciones? ¿cómo es el movimiento si b supera ese valor?
- Considere el caso particular de una partícula de masa m = 1 kg se encuentra sujeta a un muelle de constante k =1 N/m, existiendo un rozamiento b. Determine la posición en cualquier instante si se impulsa desde la posición de equilibrio con velocidad v0 = 0.6 m/s si (a) b = 1.6 N·s/m, (b) b = 2.5 N·s/m, (c) b = 2.0 N·s/m.





