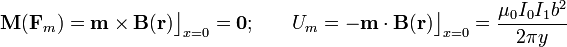Pequeña espira junto a hilo

De Laplace

Revisión a fecha de 18:54 16 jul 2008; Gabriel (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución

1 Enunciado

Un conductor cilíndrico de radio muy pequeño

a

y longitud indefinida es recorrido por una corriente continua

I 0

. Una espira cuadrada muy pequeña, de lado

b

, resistencia

R

y autoinducción despreciable, es coplanaria con el hilo y se encuentra situada a una distancia

y

de éste (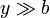 $y \gg b$ ).

Calcule, detallando los pasos, el campo magnético producido por el hilo en su exterior
Si por la espira circula una corriente $I 1$ , ¿qué fuerza ejerce el hilo sobre ella?
Suponga que la espira se aleja del hilo, sin cambiar su orientación, de modo que $y = y 0 + v 0 t$ , ¿cuánto vale la corriente $I 1$ inducida en la espira en un instante $t$ ? ¿Y la fuerza que el hilo ejerce sobre ella?

2 Solución

2.1 Campo magnético debido al hilo

Consideremos primero el hilo infinito, colineal con el eje $O Z$ , para calcular el campo de inducción magnética 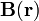$\mathbf{B}(\mathbf{r})$ creado cuando por él circula una corriente eléctrica de intensidad $I 0$ . Para ello podemos seguir dos procedimientos distintos:

2.1.1 Por integración directa

Llamemos

Λ

a nuestro conductor filiforme rectilíneo que se extiende hasta el infinito; es decir, hasta puntos suficientemente alejados de donde evaluaremos el campo. Y asumiendo que el conductor forma un circuito cerrado en el infinito, el cuál es recorrido por una intensidad de corriente

I 0

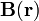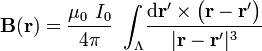
, se puede aplicar la ley de Biot y Savart para calcular el campo $\mathbf{B}(\mathbf{r})$ creado por dicha corriente: $\mathbf{B}(\mathbf{r})=\frac{\mu_0\ I_0}{4\pi}\ \int_\Lambda\!\frac{\mathrm{d}\mathbf{r'}\times\big(\mathbf{r}-\mathbf{r}'\big)}{|\mathbf{r}-\mathbf{r'}|^3}$

donde 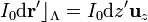$I_0 \mathrm{d}\mathbf{r'}\rfloor_\Lambda=I_0\mathrm{d}z'\mathbf{u}_z$ es el elemento de corriente en un punto $P'$ del hilo, cuya posición viene dada por 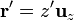$\mathbf{r'}=z'\mathbf{u}_z$ . El radiovector 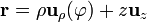$\mathbf{r}=\rho\mathbf{u}_{\rho}(\varphi)+z\mathbf{u}_z$ describe la posición del punto arbitrario $P$ donde se evalúa el campo. Operando con estas expresiones en la ecuación anterior se obtiene:

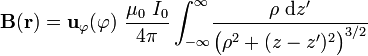
$\mathbf{B}(\mathbf{r})=\mathbf{u}_\varphi(\varphi)\ \frac{\mu_0\ I_0}{4\pi}\int_{-\infty}^\infty\!\frac{\rho\ \mathrm{d}z'}{\big(\rho^2+(z-z')^2\big)^{3/2}}$

Obsérvese que el vector unitario 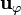$\mathbf{u}_\varphi$ sale fuera de la integral ya que sólo depende de la variable $\varphi$ , que es una de las coordenadas del punto $P(\rho,\varphi,z)$ donde se evalúa el campo y, por tanto, independiente de la variable de integración $z'$ .

La integral que aparece en al expresión anterior puede integrarse fácilmente mediante un sencillo cambio de variable, obteniéndose así el campo de inducción magnética creado por una corriente rectilínea de longitud indefinida:

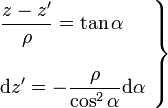
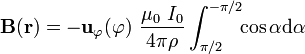
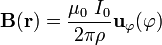
$\left.\begin{array}{l} \displaystyle \frac{z-z'}{\rho}=\tan\alpha\\ \\ \displaystyle\mathrm{d}z'=-\frac{\rho}{\cos^2\alpha}\mathrm{d}\alpha \end{array}\right\}$ $\Rightarrow$ $\mathbf{B}(\mathbf{r})=-\mathbf{u}_\varphi(\varphi)\ \frac{\mu_0\ I_0}{4\pi\rho}\int_{\pi/2}^{-\pi/2}\!\!\cos\alpha \mathrm{d}\alpha$ $\Rightarrow$ $\mathbf{B}(\mathbf{r})= \frac{\mu_0\ I_0}{2\pi\rho}\mathbf{u}_\varphi(\varphi)$

2.1.2 Por aplicación de la Ley de Ampère

Puede decirse que este segundo procedimiento goza de mayor significado físico, pero para poder aplicarlo de forma sencilla es necesario que el campo presente un alto grado de simetría. Comprobaremos primero que esto ocurre en el caso que nos ocupa. Como es bien sabido, una propiedad fundamental de 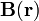$\mathbf{B}(\mathbf{r})$ es su carácter de campo solenoidal, por lo que deriva de un potencial vector 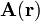$\mathbf{A}(\mathbf{r})$ que depende directamente de las fuentes del campo. En el sistema bajo estudio, ésta es la corriente rectilínea $I 0$ , de forma que...

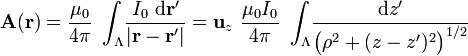
$\mathbf{A}(\mathbf{r})= \frac{\mu_0}{4\pi}\ \int_\Lambda\! \frac{I_0\ \mathrm{d}\mathbf{r}'}{|\mathbf{r}-\mathbf{r}'|}=\mathbf{u}_z\ \frac{\mu_0 I_0}{4\pi}\ \int_\Lambda\!\frac{\mathrm{d}z'}{\big(\rho^2+(z-z')^2\big)^{1/2}}$

Sin embargo no calcularemos el valor de esta integral: sólo utilizaremos el resultado de que el potencial vector generado en cualquier punto del espacio es paralelo al conductor filiforme rectilíneo; es decir, sólo tiene componente en la dirección $z$ . Por otra parte, dada la simetría cilíndrica en torno al eje $Z$ que presenta de la distribución de corriente, y su longitud infinita, permite asegurar que el valor del potencial vector en un punto sólo depende de la distancia $ρ$ que lo separa de hilo de corriente. A partir de este resultado es fácil determinar la propiedades geométricas del campo 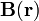$\mathbf{B}(\mathbf{r})$ :

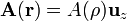
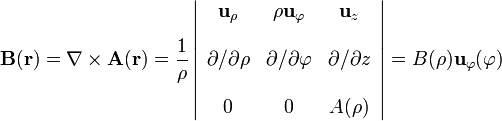
$\mathbf{A}(\mathbf{r})=A(\rho)\mathbf{u}_z$ $\Rightarrow$ $\mathbf{B}(\mathbf{r})=\nabla\times\mathbf{A}(\mathbf{r})=\frac{1}{\rho}\left|\begin{array} {ccc}\mathbf{u}_{\rho} & \rho \mathbf{u}_{\varphi} & \mathbf{u}_z \\ \\ \partial/\partial\rho & \partial/\partial\varphi & \partial/\partial z \\ \\ 0 & 0 & A(\rho) \end{array}\right|=B(\rho)\mathbf{u}_\varphi(\varphi)$

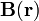Tomemos, por tanto, una circunferencia $\partial\Sigma$ de radio arbitrario $ρ$ , centrada en un punto cualquiera del eje $O Z$ y contenida en un plano perpendicular a dicho eje. La ley de Ampère establece que la circulación del campo $\mathbf{B}(\mathbf{r})$ sobre la curva $\partial\Sigma$ es proporcional a la intensidad de corriente que atraviesa cualquier superficie que se apoye en dicha curva; en el caso que nos ocupa esta intensidad es $I 0$ :

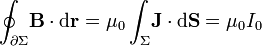
$\oint_{\partial\Sigma}\!\mathbf{B}\cdot\mathrm{d}\mathbf{r}=\mu_0\int_\Sigma\!\mathbf{J}\cdot\mathrm{d}\mathbf{S}=\mu_0I_0$

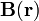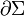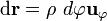Y teniendo en cuenta la simetría del campo $\mathbf{B}(\mathbf{r})$ y que el vector elemento de arco sobre la curva $\ \partial\Sigma\$ es $\ \mathrm{d}\mathbf{r}=\rho\ d\varphi\mathbf{u}_\varphi$ , se obtiene:

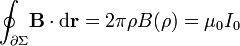
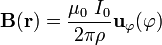
$\oint_{\partial\Sigma}\!\mathbf{B}\cdot\mathrm{d}\mathbf{r}=2\pi \rho B(\rho)=\mu_0I_0$ $\Rightarrow$ $\mathbf{B}(\mathbf{r})= \frac{\mu_0\ I_0}{2 \pi\rho}\mathbf{u}_\varphi(\varphi)$

2.2 Fuerza sobre la espira

Tal como se indica en la figura del enunciado, consideraremos que la pequeña espira cuadrada recorrida por una intensidad $I 1$ se encuentra en el plano $x = 0$ , con su centro a una distancia $y$ del hilo recorrido por la corriente $I 0$ . Para calcular la fuerza que ésta ejerce sobre la espira $Γ$ podemos utilizar la expresión,

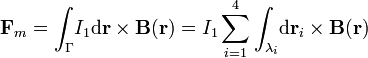
$\mathbf{F}_m=\int_{\Gamma}\!I_1\mathrm{d}\mathbf{r}\times\mathbf{B}(\mathbf{r})= I_1\sum_{i=1}^4\int_{\lambda_i}\!\mathrm{d}\mathbf{r}_i\times\mathbf{B}(\mathbf{r})$

donde 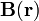$\mathbf{B}(\mathbf{r})$ es el campo de inducción creado por la corriente rectilínea y calculado en el apartado anterior, y que ha de ser evaluado en los puntos de la espira $Γ$ , es decir, en el plano $x = 0$ , o lo que lo mismo, para valores 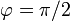$\varphi=\pi/2$ . La integral cerrada a lo largo de la espira $Γ$ se descompone en cuatro integrales sobre sus respectivos lados $λ i$ .

En los lados horizontales,

λ 1

y

λ 3

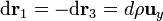, los diferenciales de camino son $\mathrm{d}\mathbf{r}_1=-\mathrm{d}\mathbf{r}_3=d\rho\mathbf{u}_y$ , con la variable

ρ

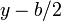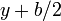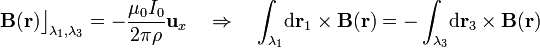
comprendida entre los valores $\, y-b/2\$ e $\ y+b/2$ ; por su parte, el campo magnético varía de forma idéntica a lo largo de dichos tramos, de manera que... $\mathbf{B}(\mathbf{r})\big\rfloor_{\lambda_1,\lambda_3}=-\frac{\mu_0I_0}{2\pi \rho}\mathbf{u}_x\quad\Rightarrow\quad\int_{\lambda_1}\!\mathrm{d}\mathbf{r}_1\times\mathbf{B}(\mathbf{r})=-\int_{\lambda_3}\!\mathrm{d}\mathbf{r}_3\times\mathbf{B}(\mathbf{r})$

En consecuencia, estos dos términos cancelarán sus contribuciones a la fuerza resultante 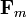$\mathbf{F}_m$ .

Los diferenciales de camino en los lados verticales, $λ 2$ y $λ 4$ , son 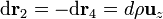$\mathrm{d}\mathbf{r}_2=-\mathrm{d}\mathbf{r}_4=d\rho\mathbf{u}_z$ , con $z$ variando entre los valores $z 0$ y $z 0 + b$ . El campo magnético es constante a lo largo de los lados verticales, pero con valores distintos en cada uno de ellos, pues se hallan a diferente distancia del conductor filiforme:

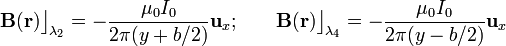
$\mathbf{B}(\mathbf{r})\big\rfloor_{\lambda_2}=-\frac{\mu_0I_0}{2\pi (y+b/2)}\mathbf{u}_x\mbox{;}\qquad\mathbf{B}(\mathbf{r})\big\rfloor_{\lambda_4}=-\frac{\mu_0I_0}{2\pi (y-b/2)}\mathbf{u}_x$

En consecuencia, sólo la acción del campo magnético sobre los lados verticales tiene una contribución neta a la resultante de la fuerza sobre la espira. Así, se tendrá que...

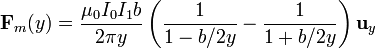
$\mathbf{F}_m=I_1\left[\int_{\lambda_2}\!\mathrm{d}\mathbf{r}_2\times \mathbf{B}+\int_{\lambda_4}\!\mathrm{d}\mathbf{r}_4\times \mathbf{B}\right]$ $\longrightarrow$ $\quad \mathbf{F}_m(y)=\frac{\mu_0I_0I_1b}{2\pi y}\left(\frac{1}{1-b/2y}-\frac{1}{1+b/2y}\right)\mathbf{u}_y$

Éste es el valor exacto de la fuerza sobre la espira, en función de la distancia del centro de ésta al conductor filiforme de longitud indefinida. Pero utilicemos el hecho de que dicha distancia es siempre mucho mayor que las dimensiones de la espira (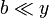 $b\ll y$ ): realizando un desarrollo en serie para 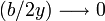$(b/2y)\longrightarrow 0$ y quedándonos con los dos primeros términos, se obtiene:

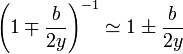
$\left(1\mp\frac{b}{2y}\right)^{-1}\simeq 1\pm \frac{b}{2y}$ $\Rightarrow$ $\displaystyle\mathbf{F}_m(y)\simeq\frac{\mu_0I_0I_1b}{2\pi y}\left[\left(1+\frac{b}{2y}\right)-\left(1-\frac{b}{2y}\right)\right]\mathbf{u}_y=\frac{\mu_0I_0I_1b^2}{2\pi y^2}\mathbf{u}_y$

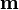Este mismo resultado puede obtenerse directamente considerando a la espira como un dipolo magnético ideal (puntual), debido a su reducido tamaño en relación con la distancia a la corriente rectilínea $I 0$ que genera el campo $\mathbf{B}$ . Como $Γ$ es una espira plana, contenida en el plano $x = 0$ y recorrida en sentido antihorario por la corriente $I 1$ , su momento dipolar magnético $\mathbf{m}$ es:

$\mathbf{m}=I_1S\mathbf{n}=I_1b^2\mathbf{u}_x$

Considerando a la espira como un ente vectorial puntual (dipolo mangético de momento 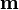$\mathbf{m}$ ) que se encuentra en todo momento en el plano $x = 0$ y orientado perpendicularmente a éste, la fuerza de interacción del campo $\mathbf{B}$ sobre ella será:

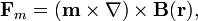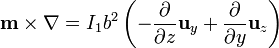
$\mathbf{F}_m=\left(\mathbf{m}\times\nabla\right)\times\mathbf{B}(\mathbf{r})\mbox{,}$ con $\mathbf{m}\times\nabla=I_1b^2\left(-\frac{\partial}{\partial z}\mathbf{u}_y+\frac{\partial}{\partial y}\mathbf{u}_z\right)$

El campo de inducción magnética que actúa sobre el dipolo es también perpendicular a dicho plano y su intensidad sólo depende del valor de la coordenada $y$ . Utilizando coordenadas cartesianas obtenemos la expresión para la fuerza ejercida sobre el dipolo magnético puntual:

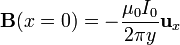
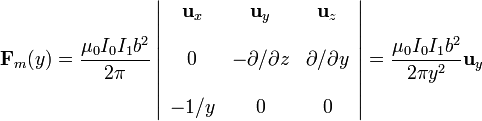
$\mathbf{B}(x=0)=-\frac{\mu_0I_0}{2\pi y}\mathbf{u}_x$ $\Rightarrow$ $\mathbf{F}_m(y)=\frac{\mu_0I_0I_1b^2}{2\pi}\left|\begin{array} {ccc}\mathbf{u}_x & \mathbf{u}_y & \mathbf{u}_z \\ \\ 0 & -\partial/\partial z & \partial/\partial y \\ \\ -1/y & 0 & 0 \end{array}\right|=\frac{\mu_0I_0I_1b^2}{2\pi y^2}\mathbf{u}_y$

Como puede comprobarse, es indéntica a la aproximación obtenida anteriormente para la fuerza magnética sobre una pequeña espira. Por otra parte, obsérvese que, al tener igual dirección el campo $\mathbf{B}$ y el momento dipolar de la espira, el par de fuerzas sobre ésta es. 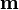Sin embargo, si las intensidades de corriente tienen el sentido propuesto en las figuras, la energía potencial del dipolo en cada punto del plano $x = 0$ tendrá su valor máximo en dicho punto; es decir, se trataría de una situación de equilibrio inestable de forma que, a la menor perturbación, aparecería un par actuando sobre la espira el cuál intentará alinear el momento dipolar magnético $\mathbf{m}$ con igual dirección y sentido que el campo exterior $\mathbf{B}$ :

$\mathbf{M}(\mathbf{F}_m)=\mathbf{m}\times\mathbf{B}(\mathbf{r})\big\rfloor_{x=0}=\mathbf{0}\mbox{;}\qquad U_m=-\mathbf{m}\cdot\mathbf{B}(\mathbf{r})\big\rfloor_{x=0}=\frac{\mu_0I_0I_1b^2}{2\pi y}$

2.3 Caso de una espira en movimiento

Pequeña espira junto a hilo

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Campo magnético debido al hilo

2.1.1 Por integración directa

2.1.2 Por aplicación de la Ley de Ampère

2.2 Fuerza sobre la espira

2.3 Caso de una espira en movimiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES